二次関数の面積を求めるとき、「交点を出して積分して…」という手順が面倒だと感じたことはありませんか。実は、放物線には “1/6公式” と呼ばれる強力な方法があり、解と係数の関係だけで面積を一瞬で求めることができます。
この公式は暗記するより、いつでも導けるようにしておく方が確実で応用も利きます。特に、二次方程式の解を実際に求めなくても積分が実行できる点が最大の魅力です。
この記事では、1/6公式の意味・証明・使い方を図解と例題付きで丁寧に解説します。
放物線と直線で囲まれた面積:1/6公式
まず、扱う公式は次の形です。
$$\int_{\alpha}^{\beta}(x-\alpha)(x-\beta)\, dx=-\frac{1}{6}(\beta-\alpha)^3$$
ここでは、次の2つの疑問を解消します。
- 面積なのになぜマイナスがつくのか?
- どうしてこれが放物線と直線で囲まれた面積になるのか?
面積のはずなのにマイナスがつく理由
結論から言うと、
- 求めている領域が $x$ 軸より下にあるから
です。

$\alpha<x<\beta$ の範囲では
$(x-\alpha)(x-\beta)$ は常に負。
負の値を積分すれば当然負になります。
したがって、実際に面積を求める際には、
$$S=\frac{1}{6}(\beta-\alpha)^3$$
です。
どこに「直線」の要素があるのか?
被積分関数
$$(x-\alpha)(x-\beta)$$
は、実は 放物線と直線 $y=0$ の差 を表しています。
面積として扱うには
(上の関数) $-$ (下の関数)
にする必要があるので、
\begin{eqnarray}
S &=& \int_\alpha^\beta\{0-(x-\alpha)(x-\beta)\}\, dx\\
&=& \frac{1}{6}(\beta-\alpha)^3
\end{eqnarray}
となります。
証明:平行移動すると一気に簡単になる
1/6公式は、展開して積分しても求まりますが、平行移動を使うと構造が一気に見えるようになります。
平行移動のイメージ
積分区間 $[\alpha,\beta ]$ を
左端が $0$ になるように平行移動すると、被積分関数は次のように整理できます。
\begin{eqnarray}
S &=& \int_\alpha^\beta(x-\alpha)(x-\beta)\,dx\\
&=& \int_0^{\beta-\alpha} x\{x-(\beta-\alpha)\}\, dx
\end{eqnarray}
証明
\begin{eqnarray}
S &=& \int_{\alpha}^{\beta}(x-\alpha)(x-\beta)\,dx\\
&=& \int_0^{\beta-\alpha}x\{x-(\beta-\alpha)\}\,dx\\
&=& \int_0^{\beta-\alpha}\{x^2-x(\beta-\alpha)\}\,dx\\
&=& \left[\frac{1}{3}x^3-\frac{1}{2}x^2(\beta-\alpha)\right]_0^{\beta-\alpha}\\
&=& -\frac{1}{6}(\beta-\alpha)^3
\end{eqnarray}
この形を毎回たどることで、
- なぜマイナスがつくのか
- なぜ係数が1/6なのか
- なぜ三乗になるのか
- 二次の係数 $a$ が付けば単に $a$ 倍になる理由
が自然に理解できます。
例題1. 解と係数の関係が威力を発揮する
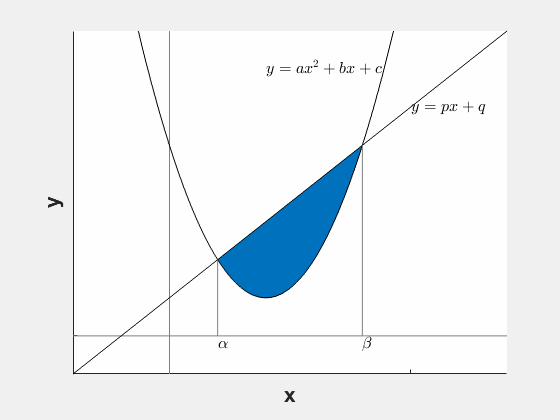
放物線 $y=x(x-3)$ と直線 $y=x-2$ とで囲まれた部分の面積 $S$ を求めよ。

求める面積は図の青で塗られている部分であり、直線の式から放物線の式を引けばよいです。
「解と係数の関係」を使うと一瞬で解ける
交点は
$$x(x-3)=x-2\; \Leftrightarrow\; x^2-4x+2=0$$
解を $\alpha,\;\beta$ とすると、
$$\alpha+\beta=4,\quad\alpha\beta=2$$
求める面積 $S$ は、
\begin{eqnarray}
S&=&\frac{1}{6}(\beta -\alpha)^3\\
&=&\frac{1}{6}\left\{\sqrt{(\alpha +\beta)^2-4\alpha\beta}\right\}^3\\
&=&\frac{1}{6}\left\{\sqrt{8}\right\} ^3\\
&=&\frac{8\sqrt{2}}{3}
\end{eqnarray}
解を実際に求めるとどうなるか
$$x=2\pm\sqrt{2}$$
これを積分に代入すると計算が非常に重く、1/6公式のありがたみがよく分かります。
例題2. 最大最小問題でも見通しが良くなる
放物線
$$y=x(x-3)$$
と直線
$$y=m(x-2)$$
で囲まれた面積 $S$ が最小となる $m$ を求めよ。
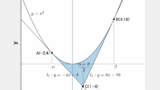
先ほどはこの問題の $m=1$ のケースを考えたことになっています。$m$ が動けば直線は動きます。下記のようです。右図は横軸に $m$ の値を、縦軸に面積 $S$ を取ったグラフです。最小値を持つことが分かります。
このイメージが持てれば、解答は先ほどの $m=1$ の場合とほぼ同じです。
解と係数の関係が威力を発揮する
交点は
$$x^2-(m+3)x+2m=0$$
解と係数の関係より
$$\alpha+\beta=m+3,\quad\alpha\beta=2m$$
面積は
$$S=\frac{1}{6}(\beta-\alpha)^3$$
だが、
\begin{eqnarray}
(\beta-\alpha)^2 &=& (\alpha+\beta)^2-4\alpha\beta\\
&=& (m+3)^2-4\cdot 2m\\
&=& (m-1)^2+8\\
\end{eqnarray}
となり、最小値は $m=1$ のとき。
面積もすぐに分かる
$m=1$ の時の面積を求めてみます。このとき、
$$\beta-\alpha=\sqrt{8}$$
なので、
$$S=\frac{1}{6}\sqrt{8}^3=\frac{8\sqrt{2}}{3}$$
まとめ:1/6公式は「解と係数の関係」と組み合わせてこそ真価を発揮する
放物線と直線で囲まれた面積は、
$$S = \frac{1}{6}(\beta-\alpha)^3$$
というシンプルな形で求められます。
この公式の本質は次の3点です。
- 面積が負になる理由:被積分関数が負なので、符号を反転して面積として扱う
- 平行移動で導出できる:$\alpha\rightarrow 0$ に平行移動することで計算が一気に簡単になる
- 解と係数の関係と相性が抜群:解を実際に求めなくても、$\alpha+\beta$ と $\alpha\beta$ から差を導ける
例題で見たように、1/6公式は
二次方程式の解を求めずに面積を出す
という強力なショートカットです。
ただし、これはあくまでも “計算のテクニック”。本質的には積分を正しく設定すれば必ず答えにたどり着けます。
さらに、1/3公式や1/12公式もあるので、ぜひ合わせて活用してみてください。



コメント