入試でよく出る二次関数の面積問題を、計算量を大幅に減らして解ける時短公式です。 ただし、丸暗記しても応用が利かないため、この記事では 公式の意味(具体例)と導出の流れ を丁寧に解説します。 1/6公式とのつながりも押さえながら、放物線の面積を体系的に理解していきましょう。実はすべて接線なので、必ず平方の形が現れます。
1/3公式:放物線と接線と壁で囲まれた面積
具体例
放物線とその接線が一点で接しており、その接点を端点とする領域の面積 $S$ は次の形になります。
$$S=\frac{1}{3}(\beta-\alpha)^3$$
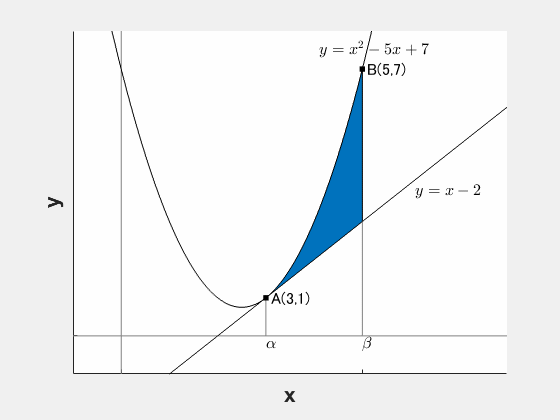
上の例だと、
$$S=\frac{1}{3}(5-3)^3=\frac{8}{3}$$
です。これはしかしながら、積分を用いてもあまり苦労はしないかもしれません。
\begin{eqnarray}
S &=& \int_3^5\left\{(x^2-5x+7)-(x-2)\right\}\,dx\\
&=& \int_3^5(x-3)^2\,dx\\
&=& \frac{1}{3}\left[(x-3)^3\right]_3^5\\
&=&\frac{8}{3}
\end{eqnarray}
接線なので、必ず平方の形が現れます。
証明
式変形のイメージ
面積は
(上の曲線)$-$(下の直線)
を $\alpha$ から $\beta$ まで積分すればよいです。このとき、接線の性質から放物線と直線との差は
$$(x-\alpha)^2$$
という “きれいな平方の形” に整理できるのがポイント。下記の動画で見るように、引き算した結果は $x$ 軸に接する放物線となるからです。
証明
\begin{eqnarray}
S &=& \int_\alpha^\beta \{(x^2+bx+c)-(px+q)\}\,dx\\
&=& \int_\alpha^\beta (x-\alpha)^2\,dx\\
&=& \frac{1}{3}\left[(x-\alpha)^3\right]_\alpha^\beta\\
&=& \frac{1}{3}(\beta-\alpha)^3
\end{eqnarray}
上の具体例の計算と見比べてください。一般形でも同じことをしていることが分かると思います。
1/12公式_その1:放物線と2つの接線で囲まれた面積
具体例
1つの放物線と2つの接線を考えます。
このとき、これらで囲まれた領域の面積 $S$ は次の形になります。
$$S=\frac{1}{12}(\beta-\alpha)^3$$
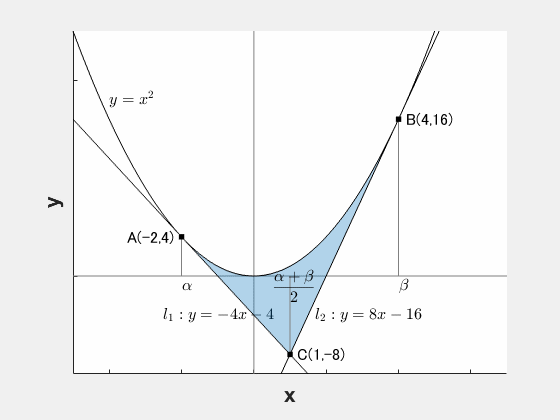
上の例だと、
$$S=\frac{1}{12}\{4-(-2)\}^3=\frac{\cancel{6\times 6}3}{\cancel{12}}\times 6=18$$
です。積分で求める場合、
\begin{eqnarray}
S &=& \int_{-2}^1\{x^2-(-4x-4)\}\,dx+\int_1^4\{x^2-(8x-16)\}\,dx\\
&=& \int_{-2}^1(x+2)^2\,dx + \int_1^4(x-4)^2\,dx\\
&=& \frac{1}{3}\left[(x+2)^3\right]_{-2}^1+\frac{1}{3}\left[(x-4)^3\right]_1^4\\
&=& \frac{1}{12}\{4-(-2)\}^3\\
&=& 18
\end{eqnarray}
です。接線なので、必ず平方の形が現れます。
でも、少し途中の計算を飛ばしました。次の証明にも役に立つので、ここでは計算を丁寧にしておきます。
途中の計算を丁寧に
\begin{eqnarray}
&&\left[(x+2)^3\right]_{-2}^1+\left[(x-4)^3\right]_1^4\\
&&=(1+2)^3-(1-4)^3=\left(\frac{-2+4}{2}+2\right)^3-\left(\frac{-2+4}{2}-4\right)^3\\
&&=\left(\frac{4-(-2)}{2}\right)^3+\left(\frac{4-(-2)}{2}\right)^3=2\,\left(\frac{4-(-2)}{2}\right)^3\\
&&=\frac{1}{4}\{4-(-2)\}^3
\end{eqnarray}
$1=\displaystyle\frac{-2+4}{2}$ です。$\alpha$ と $\beta$ の中点です。
これに係数の $\displaystyle\frac{1}{3}$ を掛けると、
$$\frac{1}{12}\{4-(-2)\}^3$$
になります。
証明
点 $\mathrm{C}$ の $x$ 座標は $\displaystyle\frac{\alpha+\beta}{2}$ になる
具体例で求めてみる
一般形で証明する前に、上記の図(下記に再掲)の具体例で求めてみます。

接線を求めれば、
- $l_1:\; y=-4x-4$
- $l_2:\; y=8x-16$
より、$\mathrm{C}(1,-8)$ となり、確かに $\alpha=-2$ と $\beta=4$ の中点です。
一般形で求める
では一般形で求めます。
- 放物線:$f(x)=ax^2$
- 接点: $\mathrm{A}(\alpha,a\alpha^2)$, $\mathrm{B}(\beta,a\beta^2)$
と置きます。放物線の一般形は $f(x)=ax^2+bx+c$ ですが、平行移動すればすべて $f(x)=ax^2$ になるのでこのように置いても一般性を失いません。また、$a>0$ としておきます。このとき、
- $l_1:\; y=2a\alpha(x-\alpha)+a\alpha^2$
- $l_2:\; y=2a\beta(x-\beta)+a\beta^2$
より、
\begin{eqnarray}
2a\beta(x-\beta)+a\beta^2 &=& 2a\alpha(x-\alpha)+a\alpha^2\\
2a(\beta-\alpha)x &=& a(\beta^2-\alpha^2)\\
\therefore\;x &=& \frac{\alpha+\beta}{2}
\end{eqnarray}
となります。
証明
$l_1$ を $y=p_1x+q_1$, $l_2$ を $y=p_2x+q_2$ とすると、
\begin{eqnarray}
S &=& \int_\alpha^\frac{\alpha+\beta}{2} \{x^2-(p_1x+q_1)\}\,dx\\
&& +\int_\frac{\alpha+\beta}{2}^\beta \{x^2-(p_2x+q_2)\}\,dx\\
&=& \int_\alpha^\frac{\alpha+\beta}{2} (x-\alpha)^2\,dx + \int_\frac{\alpha+\beta}{2}^\beta (x-\beta)^2\,dx\\
&=& \frac{1}{3}\left[(x-\alpha)^3\right]_\alpha^\frac{\alpha+\beta}{2} + \frac{1}{3}\left[(x-\beta)^3\right]_\frac{\alpha+\beta}{2}^\beta\\
&=& \frac{1}{12}(\beta-\alpha)^3
\end{eqnarray}
接線なので、必ず平方の形が現れます。
最後の式変形は、具体例のところの式変形を参考に、やってみてください。
1/12公式_その2:2つの放物線との共通接線で囲まれた面積
具体例
2つの放物線が同じ直線に接している状況を考えます。
このとき、2つの接点を端点とする領域の面積 $S$ は次の形になります。ただし、2つの放物線の二次の係数(=開き具合)が同じであることが条件です。
$$S=\frac{1}{12}(\beta-\alpha)^3$$
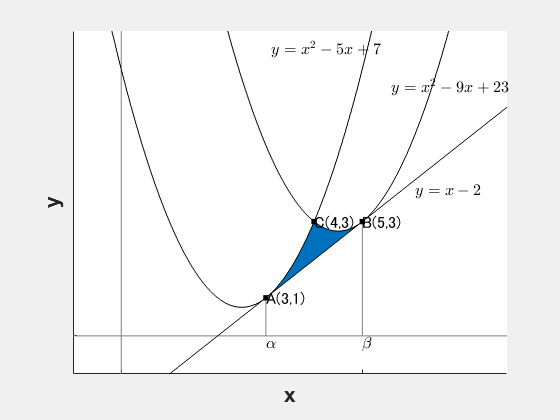
上の例だと、
$$S=\frac{1}{12}(5-3)^3=\frac{2}{3}$$
です。積分で求める場合、
\begin{eqnarray}
S &=& \int_3^4\left\{(x^2-5x+7)-(x-2)\right\}\,dx\\
&&+\int_4^5\left\{(x^2-9x+23)-(x-2)\right\}\,dx\\
&=& \int_3^4(x-3)^2\,dx + \int_4^5(x-5)^2\,dx\\
&=& \frac{1}{3}\left[(x-3)^3\right]_3^4+\frac{1}{3}\left[(x-5)^3\right]_4^5\\
&=& \frac{1}{12}(5-3)^3\\
&=& \frac{2}{3}
\end{eqnarray}
です。接線なので、必ず平方の形が現れます。
でも、少し途中の計算を飛ばしました。次の証明にも役に立つので、ここでは計算を丁寧にしておきます。
途中の計算を丁寧に
\begin{eqnarray}
&&\left[(x-3)^3\right]_3^4+\left[(x-5)^3\right]_4^5\\
&&=(4-3)^3-(4-5)^3=\left(\frac{3+5}{2}-3\right)^3-\left(\frac{3+5}{2}-5\right)^3\\
&&=\left(\frac{5-3}{2}\right)^3+\left(\frac{5-3}{2}\right)^3=2\,\left(\frac{5-3}{2}\right)^3\\
&&=\frac{1}{4}(5-3)^3
\end{eqnarray}
$4=\displaystyle\frac{3+5}{2}$ です。$\alpha$ と $\beta$ の中点です。
これに係数の $\displaystyle\frac{1}{3}$ を掛けると、
$$\frac{1}{12}(5-3)^3$$
になります。
証明
式変形のイメージ
放物線が2つあるので積分を2つに分けます。それぞれの差は、平方の形
$$(x-\alpha)^2,\;(x-\beta)^2$$
に整理できます。左右対称の構造があるため、計算が非常にきれいにまとまります。
また、2つの放物線の交点の $x$ 座標は、その対称性から
$$\frac{\alpha+\beta}{2}$$
です。
証明
\begin{eqnarray}
S &=& \int_\alpha^\frac{\alpha+\beta}{2} \{(x^2+b_1x+c_1)-(px+q)\}\,dx\\
&& +\int_\frac{\alpha+\beta}{2}^\beta \{(x^2+b_2x+c_2)-(px+q)\}\,dx\\
&=& \int_\alpha^\frac{\alpha+\beta}{2} (x-\alpha)^2\,dx + \int_\frac{\alpha+\beta}{2}^\beta (x-\beta)^2\,dx\\
&=& \frac{1}{3}\left[(x-\alpha)^3\right]_\alpha^\frac{\alpha+\beta}{2} + \frac{1}{3}\left[(x-\beta)^3\right]_\frac{\alpha+\beta}{2}^\beta\\
&=& \frac{1}{12}(\beta-\alpha)^3
\end{eqnarray}
接線なので、必ず平方の形が現れます。
最後の式変形は、具体例のところの式変形を参考に、やってみてください。
補足:1/3公式と1/12公式の違いが一瞬で分かる整理(1/6公式付き)
| 公式 | 面積のとらえ方 | 公式 | 特徴 |
|---|---|---|---|
| 1/6公式 | 放物線と直線で囲まれた面積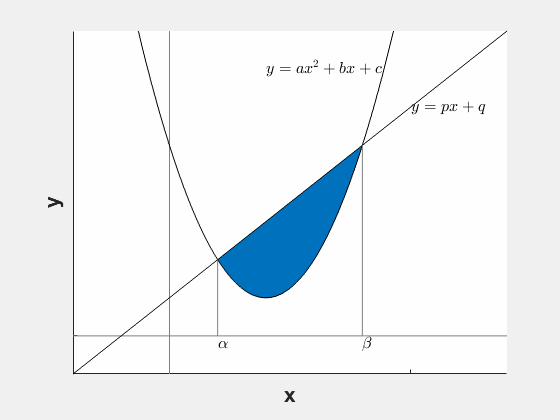 | $S=\displaystyle\frac{1}{6}(\beta-\alpha)^3$ | 解と係数の関係を用いることで、$\alpha$, $\beta$ を実際に求めなくても計算できるのがミソ。 |
| 1/3公式 | 放物線と接線と壁で囲まれた面積 | $S=\displaystyle\frac{1}{3}(\beta-\alpha)^3$ | 差が $(x-\alpha)^2$ の形になり、そのまま積分できる |
| 1/12公式 | 放物線と2つの接線で囲まれた面積 | $S=\displaystyle\frac{1}{12}(\beta-\alpha)^3$ | 直線の交点は $x=\displaystyle\frac{\alpha+\beta}{2}$ となる。 左右で積分を分けると $(x-\alpha)^2$ と $(x-\beta)^2$ が現れ、そのまま積分できる |
| 1/12公式 | 2つの放物線と共通接線で囲まれた面積 | $S=\displaystyle\frac{1}{12}(\beta-\alpha)^3$ | 放物線の交点は $x=\displaystyle\frac{\alpha+\beta}{2}$ となる。 左右で積分を分けると $(x-\alpha)^2$ と $(x-\beta)^2$ が現れ、そのまま積分できる |
まとめ:3つの面積公式はどれも自分で簡単に導ける
1/3公式と1/12公式は、1/6公式と同じく、放物線の面積を簡単に求めるための方法です。
この記事で押さえたポイントは次の3つです。
- 公式は丸暗記ではなく、仕組みを理解すれば自分で導ける
接線なので、必ず平方の形が現れる。 - 3つの公式は扱う“面積の形”が異なる
1/6公式は「放物線と直線で囲まれた面積」、
1/3公式は「放物線と接線と壁で囲まれた面積」、
1/12公式は「放物線と2つの接線で囲まれた面積」「2つの放物線との共通接線で囲まれた面積」を扱うときに便利。 - 解と係数の関係と組み合わせると計算が大幅に短縮できる
1/6公式では解を求めずに面積が出せるため、入試の二次関数の面積問題で特に強い。
放物線の面積は、扱い方を整理するだけで驚くほどシンプルになります。
次は、これらの公式が実際の入試問題でどのように使われるかを確認してみてください。
✅関連記事:1/6公式の意味と導出



コメント