食塩水問題に代表される比の計算を苦手にしている人が多くいます。私もその一人でした。私はこの考え方を高校生の化学の授業で身に付けました。高校の化学では食塩水問題に近しいことを非常にたくさん計算します。そのときこの考え方を学び、そこから比の問題がスラスラと解けるようになりました。従い、これ自体は簡単な記事ですが、高校のカテゴリーにも入れました。
達人の比の書き方
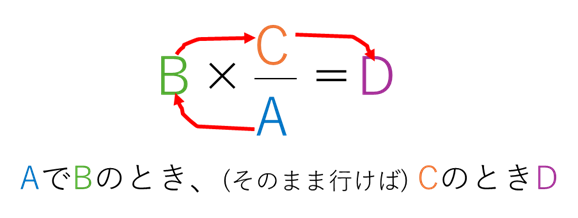
これだけ見ても何を言っているのかさっぱりだと思いますので、次に身近な例題で式の立て方とその意味を見ていきます。
例題
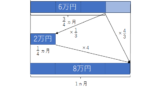
3か月で9万円稼いだ。このまま行けば1年(12か月)ではいくら稼げるか？
$$9\times\frac{12}{3}$$
という式を立てて計算し、36万円という答えを得ます。
$$9\times\frac{\cancel{12}4}{\cancel{3}}=36$$
分数の意味を理解する
(1) 月数の割り算
12か月の中に3か月は4つあるので、9万円が4回もらえるイメージです。
(2) 月給
こちらは月給を求めています。3か月で割るということは、1か月あたりを求めています。月給を12か月分得ると1年分です。
まずはこの意味を理解して、慣れれば機械的に行う
まずは、上記で述べた(1)(2)の意味をしっかりと理解しましょう。しっかりと理解できれば、あとは機械的に計算をしてOKです。意味も理解して機械的に計算できるようになれば、比の達人です。
割り算の意味については下記の記事↓でも分かりやすく述べています。こちらも見てください。
15分で6km進んだ。このまま行けば1時間(60分)ではいくら進むか？
時速を求めよ、と聞かれても答えられるように
- 1時間ではいくら進むか？
は、
- 時速何kmか？
と同じ問いです。こう聞かれても60分で進む距離を求めればよいのだな、と解釈して上述の比例式を立てましょう。このように比を立てられるようになれば、速さを求める公式
速さ $＝$ 距離 $\div$ 時間
といったものは覚える必要がありません。
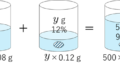
50gの食塩水の中に食塩が2g入っている。この濃度の食塩水100gの中にはいくら食塩が入っているか？
濃度を求めよ、と聞かれても答えられるように
- 食塩水100gではいくら入っているか？
は、
- 食塩水の濃度はいくらか？
と同じ問いです。濃度とは、食塩水100g当たりに入っている食塩の重さです。今は塩なので食塩水ですが、砂糖でもミョウバンでもなんでもよいです。なので、一般に食塩水にあたる言葉として溶液という言葉を使います。ちなみに、食塩は溶質、水は溶媒です。
相似
？を求めよ。
このくらいの問題なら目の子で分かりますが、例題としてあえて比の達人方式で求めます。
相似ということで次の比例式を書く人がほとんどだと思います。
$$3:6=4:x$$
ここから
$$3x=24$$
として、$x=8$ とすると。この行数と思考の長さはもったいないので、分数式1行で済ませたいです。
まとめ
比の立て方のコツを簡単な例題で示してきました。特に食塩水問題は苦手にしている人も多いのではないかと思います。この比の立て方を使えば、食塩水問題は非常に簡単に解くことができます。
この投稿でそのコツをつかんだ人は、続けて実践編でさらに力をつけてください。
リンク先執筆中！
コメント