余弦定理って、公式だけ覚えようとすると微妙に覚えにくくありませんか? 公式の気持ちを理解すれば自然に思い出せます。さらに、図形による証明はとても美しいので、一度見ておくと理解が深まります。
余弦定理:$c^2=a^2+b^2-2ab\cos\theta$

気持ち:三平方の定理を微調整するだけ
まずは大雑把な気持ちから入ります。これは 三平方の定理 の「直角三角形の世界」を出発点にすると分かりやすいです。
直角三角形と比べる
直角三角形($\theta=90^\circ$)を基本形とします。辺 $a$, $b$ の長さはそのままに、角度を$\theta<90^\circ$ にすると、向かい側の辺 $c’$ は直角のときの $c$ よりも短くなります。

短くなる “調整項 (hogehoge) ” はいくらか?
問題は、$c$ と $c’$ の差、つまり短くなる分(調整項)がいくらかです。
調整項 $ab$
三角形全体が大きくなれば $c$ も $c’$ も比例して大きくなるので、調整項は$ab$ に比例するはずです。よって、
$c’^2=a^2+b^2-(\text{調整項})\times$ $ab$
という形が自然です。
調整項 $\cos\theta$
さらに「余弦定理」という名前からも分かるように、角度による調整は $\cos\theta$ が担います。よって、
$c’^2=a^2+b^2-(\text{調整項})\times$ $ab$ $\cos\theta$
と予想できます。実際、$\theta=90^\circ$ なら $\cos\theta=0$ なので三平方の定理に戻り、気持ちとしても納得できます。
調整項 $2$
最後に残るのは定数項の $2$ですが、これは覚えておく必要があります。ただし後の図形証明やベクトル証明を見ると、この $2$ が自然に現れるので思い出しやすくなります。
こうして、
$c’^2=a^2+b^2-$ $2$ $ab$ $\cos\theta$
という形が「三平方の定理に余弦の調整項がついたもの」として理解できます。
図形による証明:アニメーションで理解
三平方の定理のアニメーションを基本形として、そこに調整項がどう現れるかを見ます。
証明動画
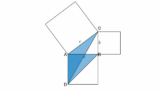
三平方の定理のアニメーションとほぼ同じですが、角度が直角でないために隙間が生まれる点が異なります。この隙間こそが調整項です。
隙間部分だけ確認
隙間以外の部分は 三平方の定理のステップ解説 と同じなので、ここでは隙間だけに注目します。
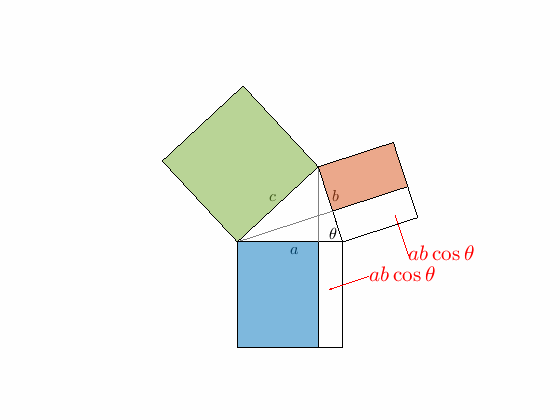
2つの隙間の面積はどちらも $ab\cos\theta$
下図で細長いほうの隙間 (四角形$\mathrm{LMEB}$) に着目すると、短い辺が $b\cos\theta$、長い辺が $a$ なので面積は
$$ab\cos\theta$$

もう一つの隙間も同じなので、2つ合わせて
$$2ab\cos\theta$$
となり、これが調整項です。
隙間の面積を引くと余弦定理
青の四角同士、赤の四角同士は同じ面積なので、隙間の分だけ引けば、
$$c^2=a^2+b^2-2ab\cos\theta$$
が得られます。
式による証明:ベクトルで一発
最後は式による証明です。これは下記記事の「大きさ問題」でも述べています。
証明
求めたいのは $|\overrightarrow{\mathrm{AB}}|^2$ なので、$\overrightarrow{\mathrm{AB}}$ を $\overrightarrow{\mathrm{OA}}$ と $\overrightarrow{\mathrm{OB}}$ で表します。

\begin{eqnarray} |\overrightarrow{\mathrm{AB}}|^2 &=& |\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}|^2\\ &=& |\overrightarrow{\mathrm{OB}}|^2 – 2\,\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}} + |\overrightarrow{\mathrm{OA}}|^2\\ &=& a^2 + b^2 – 2ab\cos\theta \end{eqnarray}
ここでも定数項の $2$ が自然に出てきます。2乗を展開したときの $2$ です。
まとめ
余弦定理を覚えるための視点を三つ紹介しました。
一つ目は気持ちで理解すること。三平方の定理を基本形とし、角度による調整項が加わると考えると自然です。
二つ目は図形による美しい証明。隙間として現れる $2ab\cos\theta$ が調整項そのものです。
最後はベクトルでの計算。図形の関係を計算に落とし込むだけで余弦定理が自然に現れます。余弦定理を覚えていなくても解ける、というのがベクトルの強みです。


コメント