空間の直線は、
「ベクトル方程式」と「軌跡方程式」の2つの視点で表すことができます。
この記事では、まずこの2つの式の意味と役割を整理し、
特に今後の記事でも繰り返し使うベクトル方程式:
基準点 + t × 方向ベクトル
という “直線の型” をしっかり身につけることを目的とします。
この型を理解しておくと、
内分点・外分点、平面との交点、点と平面の距離など、
空間ベクトルの応用が一気につながっていきます。
1. 直線の式は2種類ある
1-1. ベクトル方程式とは
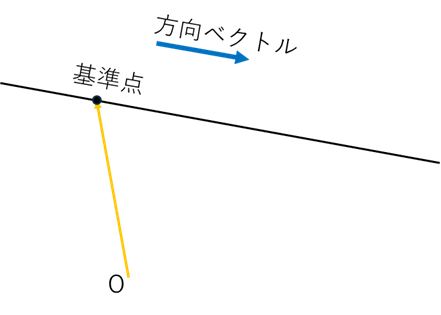
ベクトル方程式は、直線上の点を
「基準点 + $t$ × 方向ベクトル」
という形で表す式で:
- $t$ は実数
- $t$ を変えると直線上を動く点を表す
- 計算がしやすく、イメージしやすい
です。
1-2. 軌跡方程式とは
ベクトル方程式に含まれる
$t$ を消去して得られる、$x$, $y$, $z$ の関係式
です。
- 直線そのものの条件式
- 最終的な答えとして書くことが多い
$t$ を消去して得られる式が軌跡方程式であることは、下記の記事で詳しく扱っています。
1-3. どちらを使うべき?
結論はシンプルで、
- 計算 → ベクトル方程式が便利
- 最終形 → 軌跡方程式
という使い分けになります。
2. 例題:A(2,7,-1), B(3,6,0) を通る直線の式
2-1. 方向ベクトルを求める
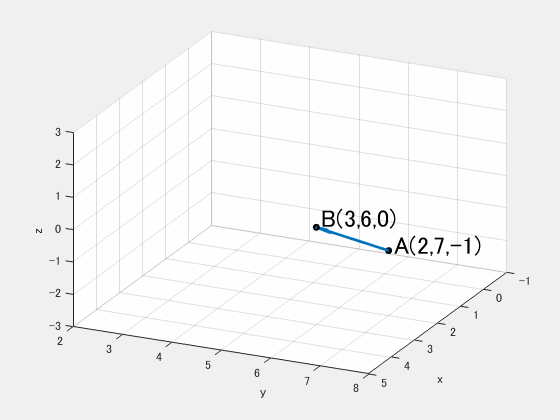
直線の向きを表す方向ベクトルは $\overrightarrow{\mathrm{AB}}$ です。
$$\overrightarrow{\mathrm{AB}}=\begin{pmatrix}3\\6\\0\end{pmatrix}-\begin{pmatrix}2\\7\\-1\end{pmatrix}=\begin{pmatrix}1\\-1\\1\end{pmatrix}$$
(図)方向ベクトルのイメージ
2-2. ベクトル方程式(点Aを基準にする)
$$\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}2\\7\\-1\end{pmatrix}
+t\begin{pmatrix}1\\-1\\1\end{pmatrix}
\tag{1}\label{p8510eq1}$$
(動画)点Aを基準にした直線の動き
2-3. ベクトル方程式(点Bを基準にする)
$$\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}3\\6\\0\end{pmatrix}+t\begin{pmatrix}1\\-1\\1\end{pmatrix}\tag{2}\label{p8510eq2}$$
(動画)点Bを基準にした直線の動き
3. 2つの式は同じ直線を表すが、t の値は異なる
基準点が違うため、
同じ点を表すときでも $t$ の値は変わります。
例として、点 $\mathrm{P}(4,5,1)$ を表す $t$ を求めてみます。
3-1. 式(1)で $\mathrm{P}$ を表すとき
$$\begin{pmatrix}2\\7\\-1\end{pmatrix}+2\begin{pmatrix}1\\-1\\1\end{pmatrix}=\begin{pmatrix}4\\5\\1\end{pmatrix}$$
→ $t = 2$
(図)式(1)で $t=2$ のとき

3-2. 式(2)で $\mathrm{P}$ を表すとき
$$\begin{pmatrix}3\\6\\0\end{pmatrix}+1\begin{pmatrix}1\\-1\\1\end{pmatrix}=\begin{pmatrix}4\\5\\1\end{pmatrix}$$
→ $t = 1$
(図)式(2)で $t=1$ のとき

3-3. 重要なポイント
ここで大事なのは、
$t$ は「点の位置を表すパラメータ」であって、 直線そのものを決めるものではない
ということです。
この考え方は、 内分点(比の計算)や平面との交点($t$ を求める)など、 後の応用でもそのまま使われます。
4. ベクトル方程式から軌跡方程式を求める
4-1. 成分表示に書き下す(式(1)を使用)
\begin{eqnarray}
x &=&& 2+t\\
y &=&& 7-t\\
z &=& -&1+t
\end{eqnarray}
4-2. $t$ を消去する
$$(t =)\; x-2 = -y+7 = z+1$$
よって軌跡方程式は
$$x-2 = -y+7 = z+1$$
4-3. 式(2)から求めても同じ式になる
点 $\mathrm{B}$ を基準にした式\eqref{p8510eq2}のベクトル方程式から $t$ を消去すると、
\begin{eqnarray}
x &=& 3+t\\
y &=& 6-t\\
z &=& 0+t
\end{eqnarray}
より、
$$x-3=-y+6=z$$
これは、一見違う式に見えますが、同じ軌跡方程式です。
例えば点 $(4,5,1)$ を代入すれば、どちらの式でも成り立ちます。
4-4. $t$ 消去の感覚をつかむ
軌跡方程式は「$t$ を消去して得られる式」ですが、 この “$t$ を消す感覚” は、
2次元で考えるとより直感的に理解できます。
次の記事では、 2次元の直線を題材にして、$t$ の消去 → 軌跡方程式 という流れをシンプルに体験していきます。
5. まとめ
- 空間の直線は ベクトル方程式 と 軌跡方程式 の2種類で表せる
- 計算ではベクトル方程式が圧倒的に便利
- 基準点が違うと $t$ の値は変わるが、直線は同じ
- 軌跡方程式は $t$ を消去して求める
次の記事では、 今回扱った「t を消去して軌跡方程式を作る」という流れを、 2次元でシンプルに理解するステップに進みます。
空間よりもイメージしやすいので、 軌跡方程式の本質がよりクリアになります。




コメント