作図パターンさえ理解すればあとは簡単な三平方の定理の問題に帰着します。円も三平方の定理も中学数学の最後の方に習うため、十分に練習する時間がない問題ですが、結構高校入試では頻出する図形なので、しっかりと慣れておきましょう。
三平方の定理をまだ習っていない人も、これは実はあまり難しくなく、下記の2つの記事でほぼばっちりになりますから、この機に先取りマスターしておきましょう。

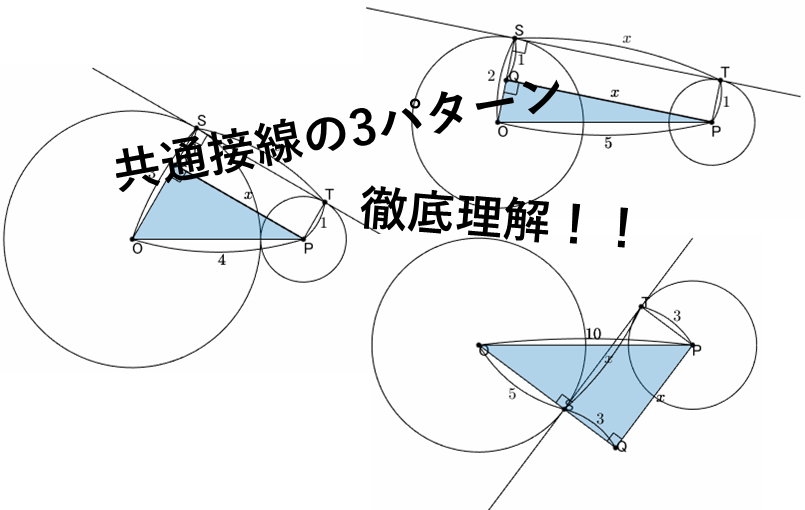
具体例3パターン
3パターン共に共通しているのは、共通接線を移動させて直角三角形を作るということです。
2円の共通外接線
$x$ を求めよ。

まずはアニメーションで全体像を把握します。
このアニメーションにより、最後は三平方の定理を用いて
\begin{eqnarray}
x^2+1^2 &=& 5^2\\
x^2 &=& 24\\
\therefore\;x&=&2\sqrt{6}\;(>0)
\end{eqnarray}
$$x=2\sqrt{6}$$
では、下記で順を追って見ていきます。
共通接線を移動させる
共通接線 $\mathrm{ST}$ を平行移動させて $\mathrm{QP}$ とします。

$$\mathrm{QS}=\mathrm{PT}=1$$
です。また三角形 $\mathrm{OPQ}$ は直角三角形です。
よって、その直角三角形に着目して三平方の定理を立てることにより、
\begin{eqnarray}
x^2+1^2 &=& 5^2\\
x^2 &=& 24\\
\therefore\;x&=&2\sqrt{6}\;(>0)
\end{eqnarray}
を得ます。

2円が外接するときの共通外接線
$x$ を求めよ。

先ほどと同じ解き方ですが、先ほどは $\mathrm{OP}$ の長さが与えられていましたが、今度はありません。でも、2円は外接しているのですから、半径の和が $\mathrm{OP}$ です。
それではまずはアニメーションで全体像を把握します。
このアニメーションにより、最後は三平方の定理を用いて
\begin{eqnarray}
x^2+2^2 &=& 4^2\\
x^2 &=& 12\\
\therefore\;x&=&2\sqrt{3}\;(>0)
\end{eqnarray}
$$x=2\sqrt{3}$$
あるいは、三平方の定理を用いるまでもなく、$90^\circ$, $60^\circ$, $30^\circ$ の直角三角形であることに気づいてもよいです。
では、下記で順を追って見ていきます。
共通接線を移動させる
共通接線 $\mathrm{ST}$ を平行移動させて $\mathrm{QP}$ とします。

$$\mathrm{QS}=\mathrm{PT}=1$$
です。また三角形 $\mathrm{OPQ}$ は直角三角形です。
よって、その直角三角形に着目して三平方の定理を立てることにより、
\begin{eqnarray}
x^2+2^2 &=& 4^2\\
x^2 &=& 12\\
\therefore\;x&=&2\sqrt{3}\;(>0)
\end{eqnarray}
を得ます。

あるいは、$2$ と $4$ の特徴的な比に気づけば、$1:2:\sqrt{3}$ の直角三角形であることがわかるので、すぐに
$$2\sqrt{3}$$
が出せます。
2円の共通内接線
$x$ を求めよ。

これも、これまでの解き方と同じです。まずはアニメーションで全体像を把握します。
このアニメーションにより、最後は三平方の定理を用いて
\begin{eqnarray}
x^2+8^2 &=& 10^2\\
x^2 &=& 36\\
\therefore\;x&=&6\;(>0)
\end{eqnarray}
$$x=6$$
これも、$3:4:5$ の直角三角形であることに気づけば、ほぼ計算せずに $x=6$ は分かります。
では、下記で順を追って見ていきます。
共通接線を移動させる
共通接線 $\mathrm{ST}$ を平行移動させて $\mathrm{QP}$ とします。また同様に半径 $\mathrm{PT}$ を平行移動させて $\mathrm{QS}$ とします。

$$\mathrm{QS}=\mathrm{PT}=3$$
です。また三角形 $\mathrm{OPQ}$ は直角三角形です。
よって、その直角三角形に着目して三平方の定理を立てることにより、
\begin{eqnarray}
x^2+8^2 &=& 10^2\\
x^2 &=& 36\\
\therefore\;x&=&6\;(>0)
\end{eqnarray}
を得ます。

これも、$3:4:5$ の直角三角形であることに気づけば強いです。
一般形3パターン
どんな数字が来ても解けるように一般形でも見てみましょう。これは公式として覚えるためではなく、どのような数字が来ても解けるよ、ということを理解するためです。
2円の共通外接線
$x$ を求めよ。

まずはアニメーションで全体像を把握します。
このアニメーションにより、最後は三平方の定理を用いて
\begin{eqnarray}
x^2+(r_1-r_2)^2 &=& d^2\\
x^2 &=& d^2-(r_1-r_2)^2\\
\therefore\;x&=&\sqrt{d^2-(r_1-r_2)^2}\;(>0)
\end{eqnarray}
$$x=\sqrt{d^2-(r_1-r_2)^2}$$
では、下記で順を追って見ていきます。
共通接線を移動させる
共通接線 $\mathrm{ST}$ を平行移動させて $\mathrm{QP}$ とします。

$$\mathrm{QS}=\mathrm{PT}=r_2$$
です。また三角形 $\mathrm{OPQ}$ は直角三角形です。
よって、その直角三角形に着目して三平方の定理を立てることにより、
\begin{eqnarray}
x^2+(r_1-r_2)^2 &=& d^2\\
x^2 &=& d^2-(r_1-r_2)^2\\
\therefore\;x&=&\sqrt{d^2-(r_1-r_2)^2}\;(>0)
\end{eqnarray}
を得ます。

2円が外接するときの共通外接線
$x$ を求めよ。

先ほどと同じ解き方ですが、先ほどは $\mathrm{OP}$ の長さが与えられていましたが、今度はありません。でも、2円は外接しているのですから、半径の和が $\mathrm{OP}$ です。
それではまずはアニメーションで全体像を把握します。
このアニメーションにより、最後は三平方の定理を用いて
\begin{eqnarray}
x^2+(r_1-r_2)^2 &=& (r_1+r_2)^2\\
x^2 &=& (r_1+r_2)^2-(r_1-r_2)^2\\
\therefore\;x&=&\sqrt{(r_1+r_2)^2-(r_1-r_2)^2}\;(>0)
\end{eqnarray}
$$x=\sqrt{(r_1+r_2)^2-(r_1-r_2)^2}$$
では、下記で順を追って見ていきます。
共通接線を移動させる
共通接線 $\mathrm{ST}$ を平行移動させて $\mathrm{QP}$ とします。

$$\mathrm{QS}=\mathrm{PT}=r_2$$
です。また三角形 $\mathrm{OPQ}$ は直角三角形です。
よって、その直角三角形に着目して三平方の定理を立てることにより、
\begin{eqnarray}
x^2+(r_1-r_2)^2 &=& (r_1+r_2)^2\\
x^2 &=& (r_1+r_2)^2-(r_1-r_2)^2\\
\therefore\;x&=&\sqrt{(r_1+r_2)^2-(r_1-r_2)^2}\;(>0)
\end{eqnarray}
を得ます。

2円の共通内接線
$x$ を求めよ。

これも、これまでの解き方と同じです。まずはアニメーションで全体像を把握します。
このアニメーションにより、最後は三平方の定理を用いて
\begin{eqnarray}
x^2+(r_1+r_2)^2 &=& d^2\\
x^2 &=& d^2-(r_1+r_2)^2\\
\therefore\;x&=&\sqrt{d^2-(r_1+r_2)^2}\;(>0)
\end{eqnarray}
$$x=\sqrt{d^2-(r_1+r_2)^2}$$
では、下記で順を追って見ていきます。
共通接線を移動させる
共通接線 $\mathrm{ST}$ を平行移動させて $\mathrm{QP}$ とします。また同様に半径 $\mathrm{PT}$ を平行移動させて $\mathrm{QS}$ とします。

$$\mathrm{QS}=\mathrm{PT}=r_2$$
です。また三角形 $\mathrm{OPQ}$ は直角三角形です。
よって、その直角三角形に着目して三平方の定理を立てることにより、
\begin{eqnarray}
x^2+(r_1+r_2)^2 &=& d^2\\
x^2 &=& d^2-(r_1+r_2)^2\\
\therefore\;x&=&\sqrt{d^2-(r_1+r_2)^2}\;(>0)
\end{eqnarray}
を得ます。

まとめ
2円の共通接線の接点間距離を求める問題も高校入試で頻出です。少し形を変えて出てくる場合もありますが、この基本パターンをしっかりと身に着けておくことで形を変えた部分に集中して考えることができるため、まずはこのパターンをしっかりと身に着けてください。


コメント