空間の直線の表し方(基礎編)では、 「基準点+t×方向ベクトル」 という直線の型を学びました。
2次元で t を消去する流れ(超基礎編)では、 t が“位置を表すパラメータ” であることを確認しました。
内分点・外分点(応用編)では、 ベクトル方程式だけで位置が求まる という統一的な見方を体験しました。
さらに、直線と平面の交点(応用編)では、 直線の式を平面に代入して t を求める という流れを学びました。
この記事では、その流れを最終的に統合して、 点と平面の距離をベクトル方程式で求める方法 を扱います。
1. 点と平面の距離の基本
点と平面の距離とは、点から平面に下ろした垂線の長さのことです。
図の $|\overrightarrow{\mathrm{PH}}|$ です。
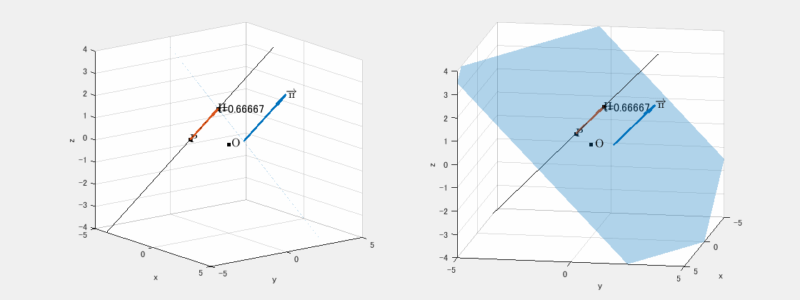
1-1. なぜ垂線を使うのか?
平面に最も近い点は、点から平面に下ろした垂線の足です。
つまり、距離=垂線の長さ というのは「最短距離の定義」そのものです。
1-2. 平面の法線ベクトルとは?
平面の式が
$$ax+by+cz=d$$
のとき、平面に垂直なベクトル(法線ベクトル)は
$$\overrightarrow{n}=\begin{pmatrix}a\\b\\c\end{pmatrix}$$
です。
この事実を2次元で分かりやすくに説明した記事:
1-3. 距離を求める流れ(全体像)
点と平面の距離は、次の4ステップで求められます。
- ① 平面の法線ベクトルを求める
- ② 点 $\mathrm{P}$ を通り、法線方向のベクトル方程式を作る
- ③ その直線と平面の交点(パラメータ値)を求める
- ④ 距離=パラメータ値×法線ベクトルの大きさ
この4ステップは、 「点から平面に垂直に進んでいき、平面に到達するまでの距離を測る」 というイメージそのものです。
- 法線ベクトル → 垂直方向
- パラメータ値:$t$ → どれだけ進むか
- 法線ベクトルの大きさ:$|\overrightarrow{n}|$ → 単位あたりの “実際の距離”
という対応になっています。
2. ベクトル方程式で距離を求める(4ステップ)
ここからは、実際にベクトル方程式を使って距離を求めていきます。
平面 $x+2y+2z=2$ と点 $\mathrm{P}(-2,-1,0)$ との距離 $d$ を求めよ。
2-1. 平面の法線ベクトルを求める
平面の法線ベクトルは
$$\overrightarrow{n}=\begin{pmatrix}1\\2\\2\end{pmatrix}$$
2-2. 点 $\mathrm{P}$ を通り、法線方向のベクトル方程式を作る
点 $\mathrm{P}(-2,-1,0)$ から平面に垂直な直線の式は
$$ \begin{pmatrix}x\\y\\z\end{pmatrix} = \begin{pmatrix}-2\\-1\\0\end{pmatrix} + t\begin{pmatrix}1\\2\\2\end{pmatrix} $$
2-3. その直線と平面の交点(パラメータ値)を求める
平面の式 $x+2y+2z=2$ に代入して、
$$ (-2+t)+2(-1+2t)+2(2t)=2 $$
$$ -4+9t=2 $$
$$ t=\frac23 $$
2-4. 距離=パラメータ値の大きさ×法線ベクトルの大きさ
$$|\overrightarrow{n}|=\left|\begin{pmatrix}1\\2\\2\end{pmatrix}\right|=3$$
より、
$$d=\frac23\times 3=2$$
ここでの $t$ は、 点 $\mathrm{P}$ が平面に到達するまで、法線方向にどれだけ進むか を表す量です。
法線ベクトルの大きさ $|\overrightarrow{n}|$ を掛けることで、 “実際の距離” が得られます。
3. ベクトル方程式で距離を求める(例題)
平面 $x+2y+2z=4$ と点 $\mathrm{P}(5,1,3)$ との距離 $d$ を求めよ。
3-1. 解
平面の法線ベクトルを求める
平面の法線ベクトルは
$$\overrightarrow{n}=\begin{pmatrix}1\\2\\2\end{pmatrix}$$
点 $\mathrm{P}$ を通り、法線方向のベクトル方程式を作る
点 $\mathrm{P}(5,1,3)$ から平面に垂直な直線の式は
$$ \begin{pmatrix}x\\y\\z\end{pmatrix} = \begin{pmatrix}5\\1\\3\end{pmatrix} + t\begin{pmatrix}1\\2\\2\end{pmatrix} $$
その直線と平面の交点(パラメータ値)を求める
平面の式 $x+2y+2z=4$ に代入して、
$$ (5+t)+2(1+2t)+2(3+2t)=4 $$
$$ 13+9t=4 $$
$$ t=-1 $$
距離=パラメータ値の大きさ×法線ベクトルの大きさ
$$|\overrightarrow{n}|=3$$
より、
$$d=1\times 3=3$$
4. 公式とのつながり
今回の計算を整理すると、教科書に載っている「点と平面の距離の公式」が自然に導けます。
平面 $ax+by+cz+d=0$ と点 $\mathrm{P}(x_0,y_0,z_0)$ との距離 $d$ は、
$$d=\frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}}$$
ベクトル方程式で理解しておくと、公式の意味がよく分かり、忘れにくくなります。
また、忘れても上記の手順で簡単に求められます。
公式の証明は下記の記事で行っています。
5. まとめ
点と平面の距離は、次の4ステップで求められます。
- ① 平面の法線ベクトルを求める
- ② 点 $\mathrm{P}$ を通り、法線方向のベクトル方程式を作る
- ③ その直線と平面の交点(パラメータ値)を求める
- ④ 距離=パラメータ値×法線ベクトルの大きさ
この一連の記事で扱ってきた 「基準点+t×方向ベクトル」 という考え方は、 空間ベクトルの多くの問題を統一的に扱える強力な道具です。
距離・交点・内分点など、 一見バラバラに見える内容が一本につながることを実感できたと思います。
5-1. 関連記事
空間の直線の表し方(基礎編):
2次元で t を消去する流れ(超基礎編):
内分点・外分点(応用編):
直線と平面の交点(応用編):







コメント