このシリーズでは領域問題の基本を、順像法・逆像法・裏ワザ(包絡線)の3ステップで体系的に理解します。本記事(#1-1)では、まず順像法の本質である「$x$ を固定して $y$ の範囲を見る」という考え方を、ファクシミリの原理と小窓の比喩を使って “感覚レベルで理解できる” ようになります。
同じ問題を逆像法で解く #1-2 と合わせて読むことで、2つの解法の違いがより鮮明になります。
#1-2:逆像法
直線群 $y=2tx-t^2$ の通過領域を順像法で求める
まずはここで考える問題とその解答を先に示すことでゴールを明確にします。
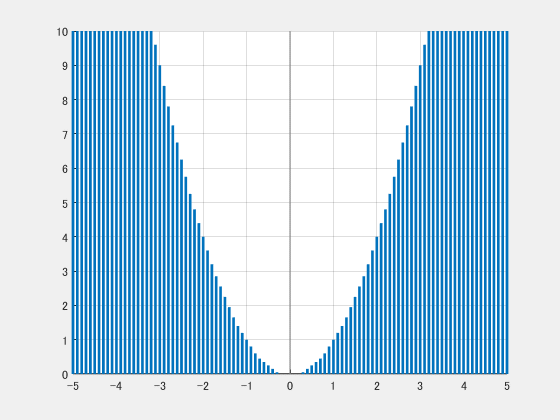
$t$ が実数全体を動くとき、直線 $y=2tx-t^2$ が通過する領域を図示せよ。
実際に通過させるとこのようになります。
解1. あっさりしすぎ?
この解法は平方完成の式変形で一発ですが、初学者には分かりにくいかもしれません。(なので解2で直感的に補う)
[解1] 直線の式を $t$ で整理して
$$\begin{eqnarray}
y&=&-t^2+2tx\\
&=&-(t-x)^2+x^2\\
&\le& x^2
\end{eqnarray}$$
よって、
$$y\le x^2$$
解2. 一時的に変数を固定する:小窓から覗く
解1は最短ルートですが、直感的には少しつかみにくいかもしれません。そこで解2では、
$x$ を固定して”小窓から覗く” ように $y$ の動きを観察する
という順像法の本質を、より具体的に体感します。
$x=X$ は小窓
[解2] $x=X$ で固定したときの $y$ の通過範囲を考える。
$$\begin{eqnarray}
y&=&-t^2+2tX\\
&=&-(t-X)^2+X^2
\end{eqnarray}$$

より、$y\le X^2$
定数 $X$ を変数 $x$ に戻して、
$$y\le x^2$$
解説. 小窓を動かして確認する:ファクシミリの原理
$X$ を固定して覗く
ファクシミリ(FAX)のように、細いスリットを動かしながら全体像を読み取るイメージです。順像法では、この
「細いスリット $= x$ を固定した小窓」を少しずつ動かしながら領域全体を把握
します。
$X$ を固定しながらも覗く窓を変えていく
上記で固定した $X$ を少しずつ動かして同じように覗いていきます。時間がかかるので先ほどの絵よりもずいぶんと早巻きです。
【動画の見どころ】
- $x$ を固定すると、$y$ がどう動くか
- 順像法の「スキャンする」感覚がつかめる
- 小窓の意味が直感的に理解できる
最後に $X$ は「一時的に固定しただけ」なので、元の変数 $x$ に戻します。固定した値が何であっても成り立つからこそ、一般の $x$ に戻せるわけです。
まとめ
【順像法の本質まとめ】
- $x$ を一時的に固定 $(X)$ する(小窓を作る)
- その小窓の中で $y$ の最小値・最大値を調べる
- 小窓を動かして全体像を把握する
- 最終的に「固定した $X$ を元の変数 $x$ に戻す」ことで領域全体が得られる
順像法とは、ファクシミリのように
$x$ を固定して $y$ の範囲を調べ、その小窓を動かすことで領域全体をスキャンする方法
です。
順像法の理解が深まったら、次は同じ問題を逆像法で解いてみましょう。2つの解法の違いが一気にクリアになります。
#1-2:逆像法
さらに、順像法と逆像法の使い分けを整理した#2、裏技的な解法を扱う#3も合わせて読むと理解が完成します。
#2:順像法と逆像法の見比べ
#3:裏ワザ(包絡線)



コメント