【三角関数の極限】sinx/x ＝1 の直感的かつ本質的な意味をアニメーションで解説

　三角関数の極限、特に

$$\lim_{x\to 0}\frac{\sin x}{x}=1$$

は、微分の学習で突然現れる “謎公式” として、多くの人が「なぜ1になるのか？」と疑問を抱きます。教科書では証明が示されるものの、本質的な意味や直感的なイメージがつかめないまま暗記してしまうケースも少なくありません。

この記事では、この極限が

$x$ が $0$ に近いとき、$\sin x$ は $x$ とほぼ同じになる

というシンプルな事実に基づいていることを、アニメーションを使って視覚的に理解できるように解説します。さらに、

• $\displaystyle\lim_{x\to 0}\displaystyle\frac{\sin 2x}{x}$
• $\displaystyle\lim_{x\to 0}\displaystyle\frac{\tan x}{x}$
• $\displaystyle\lim_{x\to 0}\displaystyle\frac{1-\cos x}{x^2}$

といった関連する三角関数の極限も、同じ感覚で一貫して理解できるようになります。

公式を丸暗記するのではなく、「なぜそうなるのか」を腑に落としたい人のための解説です。

$\displaystyle\lim_{x\to0}\frac{\sin x}{x}=1$ の直感的理解

「$\sin x\fallingdotseq x$」という意味を表す

　結論を先に書くとこれは、

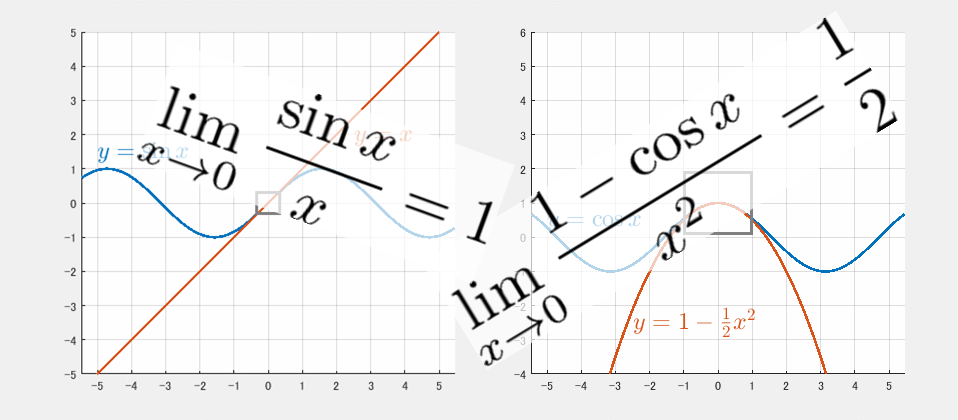
という意味です。この感覚をつかむために、$\sin\,x$ と $x$ のグラフを比較してみましょう。下のアニメーションでは、左側の□部分が徐々に $x\fallingdotseq 0$ の範囲へと縮まり、その部分を右側に拡大して表示しています。

　$\displaystyle\lim_{x\to 0}$ は「$x$ が $0$ に限りなく近づくとき」を意味します。そのとき $\displaystyle\frac{\sin x}{x}=1$ なのだから、

$$\sin x\fallingdotseq x$$

と考えてよいわけです（もちろん $x=0$ そのものではなく、あくまで $x\fallingdotseq 0$ の範囲での近似です）。

$\displaystyle\lim_{x\to0}\frac{\sin 2x}{x}=2$ の直感的理解

「$\sin 2x\fallingdotseq 2x$」という意味を表す

　同じ考え方で、この極限は

という意味です。こちらもアニメーションで確認できます。

答案に書くときの処理

　答案では、必ず $\displaystyle\lim_{x\to 0}\frac{\sin x}{x}=1$ を使って処理します。

答案

\begin{eqnarray}
\lim_{x\to 0}\frac{\sin 2x}{x} &=& \lim_{x\to 0}\frac{\sin 2x}{2x}\cdot 2\\
&&= 1\cdot 2\\
&& \; =2\\
\end{eqnarray}

$\displaystyle\lim_{x\to 0}\frac{\sin 2x}{2x} = 1$ が成り立つ理由

　$x\to 0$ なら当然 $2x\to 0$ なので、元の極限公式がそのまま使えます。

$\displaystyle\lim_{x\to0}\frac{\tan x}{x}=1$ の直感的理解

「$\tan x\fallingdotseq x$」という意味を表す

　これも同様に、

という意味です。アニメーションで確認できます。

答案に書くときの処理

答案

\begin{eqnarray}
\lim_{x\to 0}\frac{\tan x}{x} &=& \lim_{x\to 0}\frac{\sin x}{x}\cdot\frac{1}{\cos x}\\
&&= 1\cdot \frac{1}{1}\\
&&\; = 1\\
\end{eqnarray}

$\displaystyle\lim_{x\to0}\frac{1-\cos x}{x^2}=\frac{1}{2}$ の直感的理解

「$ 1-\cos x\fallingdotseq \frac{1}{2}x^2$」という意味を表す

　同じ発想で、

という近似が成り立ちます。こちらもアニメーションで確認できます。

答案に書くときの処理

答案

\begin{eqnarray}
\lim_{x\to 0}\frac{1-\cos x}{x^2} &=& \lim_{x\to 0}\frac{1-\cos x}{x^2}\cdot\frac{1+\cos x}{1+\cos x}\\
&=& \lim_{x\to 0}\frac{1-\cos^2 x}{x^2}\cdot\frac{1}{1+\cos x}\\
&=& \lim_{x\to 0}\left(\frac{\sin x}{x}\right)^2\cdot\frac{1}{1+\cos x}\\
&&= 1^2\cdot\frac{1}{1+1}\\
&&\; = \frac{1}{2}\\
\end{eqnarray}

まとめ

　微分の学習で突然現れる「謎公式」の代表である

$$\lim_{x\to 0}\frac{\sin x}{x}=1$$

について、この記事ではその直感的な意味を整理しました。要するに、

$x\fallingdotseq 0$ のとき $\sin x\fallingdotseq x$

という感覚を持つことが大事です。これは「三角関数のような複雑な関数でも、十分小さな範囲では多項式で近似できる」という事実を示しており、大学ではテイラー展開として一般化されます。

また、極限がどのように「近づいていく」のかを視覚的に理解したい場合は、こちらの記事も参考になります。