通過領域の問題を逆像法で解くときの本質は、
「その点を通る直線が存在するか?」=解の存在条件を調べることにあります。
この記事では、
- 判別式を使った最短ルート(解1)
- 点を固定して直感的に理解するルート(解2)
- 具体例 $(2,3)$ と $(2,5)$ の比較
を通して、逆像法の考え方を “感覚レベルで理解できる” ようになります。
そして、ここで扱う問題はあえて順像法と同じにしています。そのことにより両者の違いがより明確になるでしょう。
順像法はこちら↓。
直線群 $y=2tx-t^2$ の通過領域を逆像法で求める
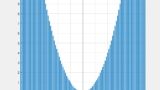
$t$ が実数全体を動くとき、直線 $y=2tx-t^2$ が通過する領域を図示せよ。
実際に通過させると次のようになります。
【動画の見どころ】
- $t$ を動かすと直線がどう変化するか
- 通過領域の “上側が欠ける理由”
- 逆像法で出てくる条件 $y\le x^2$ のイメージ
解1. あっさりしすぎ?
この解は判別式で一発ですが、初学者には分かりにくいかもしれません。(なので解2で直感的に補う)
[解1] 直線の式を $t$ で整理して
$$t^2-2xt+y=0$$
これを $t$ に関する二次方程式とみてその判別式を $D$ と置くと、$t$ が実数解を持てばよいので、
$$\begin{eqnarray}
\frac{D}{4} &=& x^2-y\\
&\ge& 0
\end{eqnarray}$$
よって、
$$y\le x^2$$
解2. 一時的に変数を固定する:通過を願う点の気持ち
解1は最短ルートですが、「なぜ判別式が出てくるのか」が直感的に理解しづらい。そこで解2では、
点を固定して “その点を通る直線が存在するか” を確かめる
という逆像法の本質を、より具体的に体験します。
点 $(X,Y)$ は $y=2tx-x^2$ の通過を願う点
[解2] 点 $(X,Y)$ を考える。この点が直線 $y=2tx-t^2$ を通るとき、$t$ に関する二次方程式
$$Y=2tX-t^2$$
$$t^2-2tX+Y=0$$
は解を持つから、この判別式を $D$ と置くと、
$$\begin{eqnarray}
\frac{D}{4} &=& X^2-Y\\
&\ge& 0
\end{eqnarray}$$
より、$Y\le X^2$
定数 $X$, $Y$ を変数 $x$, $y$ に戻して、
$$y\le x^2$$
解説. 具体的に固定して確かめてみる
【具体例の狙い】
- $(2,3)$ は実数解 → 通過する
- $(2,5)$ は虚数解 → 通過しない
この対比で “解の存在条件=通過領域” が直感的に理解できます。
$(2,3)$ に解はあるんか?
「点 $(X,Y)$ を考える」と宣言していることに注目しましょう。これは、具体的な点、例えば「点 $(2,3)$ を考える」と言っています。この状態を問題風に書くと、次のようになります。
直線 $y=2tx-t^2$ は点 $(2,3)$ を通るか? 通るなら、$t$ の値と直線の式を求めよ。
解
直線の式に点 $(2,3)$ を代入すると、
$$3=2t\times 2-t^2$$
$$t^2-4t+3=0$$
$$(t-1)(t-3)=0$$
$$\therefore\;t=1,\, 3$$
検算
点 $(2,3)$ は求める領域内にあり、確かに $t=1,\, 3$ としてそこを通る直線が存在します。

$(2,5)$ に解はあるんか?
では、点 $(2,5)$ ならどうでしょうか?
直線 $y=2tx-t^2$ は点 $(2,5)$ を通るか? 通るなら、$t$ の値と直線の式を求めよ。
解
直線の式に点 $(2,5)$ を代入すると、
$$5=2t\times 2-t^2$$
$$t^2-4t+5=0$$
解の公式を用いると、
$$\begin{eqnarray}
t &=& 2\pm\sqrt{4-5}\\
&=& 2\pm i
\end{eqnarray}$$
よって、直線は点 $(2,5)$ を通らない。
検算
点 $(2,5)$ は領域内にはなく、確かに対応する直線は存在しません。

これらからわかること
この2つの例からわかるように、具体的な点 $(X,Y)$ を直線が通るかどうかは、
$t$ に関する二次方程式が解を持つかどうか
ということになり、判別式 $D$ を調べたくなる気持ちが湧いてきます。逆像法とは、
「その点を通る直線が存在するか?」を判別式で判定する方法
であることが、ここまでの例から自然に見えてきます。
まとめ:そこに解はあるんか?
【逆像法の本質まとめ】
- 点 $(X,Y)$ を固定する
- その点を通る直線の式を立てる
- それを $t$ に対する方程式に見方を変え、$t$ が実数解を持つかどうかを判別式で調べる
- 実数解となる $(X,Y)$ の範囲が通過領域
つまり逆像法とは、
「通過領域=実数解が存在する点の集合」
という視点で問題を解く方法です。
逆像法の理解が深まったら、次は実際の入試問題で “使えるレベル” に落とし込みましょう。




コメント