運動エネルギーの公式は、多くの人が一度は見たことのある次の式です。
$$W = \frac{1}{2}mv^2-\frac{1}{2}mv_0^2$$
この記事では、この公式の中でも特に
- なぜ 1/2 が付くのか?
- なぜ速度の2乗になるのか?
- 運動量($mv$)との違いは何か?
を、できるだけ 直感的に 理解できるように解説します。
微分積分をがっつり使うというより、
「パッと見で腑に落ちる」 ことを重視します。
微分積分をがっつり使う姉妹ページも用意しています。
まずはシンプルに導いてみる
次の状況を考えます。
あなたの手が力 $F$ で質量 $m$ の物体を距離 $x$ だけ引っ張る。
その結果、速度が $v_0$ から $v$ に変化する。摩擦はない。

ここで、あなたの手が行った「仕事」$W$ は
どのような形で物体に乗り移ったのか?
等加速度運動を前提にすると、一行でこうなる
簡単のために一定の力を加えており、従って物体は等加速度運動をしているとします。

つまり、
- 仕事の定義
- 運動方程式
- 等加速度運動の式
を組み合わせて式変形すると、
自然に $\displaystyle\frac12 mv^2$ の形が現れます。
1/2 が出る理由(式変形の“意味”)
式変形としては「そうなるからそうなる」なのですが、あえて意味を解釈すると、
- 等加速度運動の公式の右辺にある「2」
- それが逆数になって「1/2」になる
という流れです。
ここで出している等加速度運動の公式は $v^2-v_0^2=2ax$ ですが、これは
- $v=v_0+at$
- $x=v_0t+\displaystyle\frac12 at^2$
から来ています。この $\displaystyle\frac12$ は、
速度を積分した結果として自然に出てくる係数
です。
その直感的理解は次の章で説明します。
1/2 の意味を直感でつかむ
ここからがこの記事の本番です。
式変形ではなく、
図と直感で「1/2 の意味」を理解する方法を紹介します。
$v–t$ グラフの三角形の面積
距離 $x$ は、$v–t$ グラフの面積で表されます。
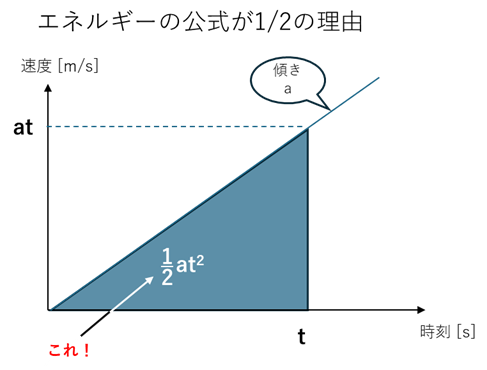
等加速度運動では $v-t$ グラフは三角形。初めは遅く、だんだん速くなる状態。
三角形の面積には $\displaystyle\frac12$ が出てくる。
つまり、
初めは遅く、だんだん速くなることを反映して「1/2」が出る
というわけです。
なぜ運動エネルギーは $v^2$ なのか?
これも直感で理解できます。
- 距離 $x$ は 時間 $t$ の2乗に比例
($x\propto t^2\;:\;v-t$ グラフの面積) - 速度 $v$ は 時間 $t$ に比例
($v\propto t\;:\;v-t$ グラフの直線)
だから、
- 距離ベースの仕事 $W=Fx$ は
距離に比例 し $(W\propto x\propto t^2)$ - 速度の 2乗に比例 する $(W\propto x\propto t^2\propto v^2)$
直感で言うなら、
等加速度で引っ張ったとき、
速度が2倍になる頃には、距離は4倍進んでいる
だから仕事は4倍している
です。
ただしこれはむしろ逆の見方の方がよいかもしれません。
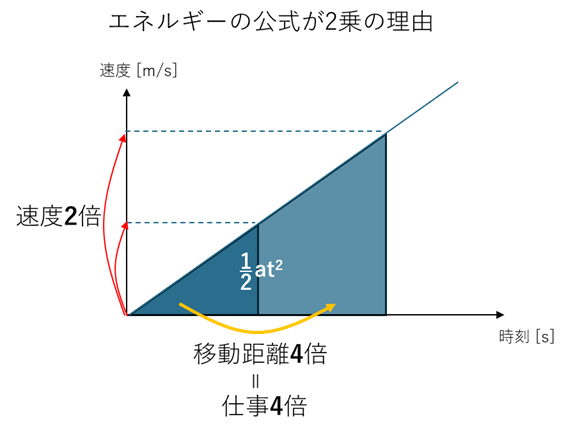
つまり、
仕事を4倍しているのに速度が2倍しか増えない
ということです。
三角形での直感で言えば、速度を増やすためには面積をいっぱい増やさないといけない、ということですね。
力が一定でない場合も $\displaystyle\frac12 mv^2$ になる
力が一定でない場合でも、
同じように仕事の定義から式変形すると
やはり $\displaystyle\frac12 mv^2$ が現れます。

つまり、
- 力が一定でも
- 力が変化しても
運動エネルギーの形は必ず $\displaystyle\frac12 mv^2$ になります。
この一般形の導出は姉妹ページで詳しく扱っています。
まとめ:力が一定の場合とそうでない場合の比較
力が一定(等加速度運動)の場合もそうでない場合も同じ結果になりました。
まとめとして両者を比較します。

力学的エネルギー保存の法則とのつながりを見る
ここまでの導出では、
仕事をしたのは「あなたの手」でした。
しかし、この仕事を 重力が行った と考えると、
そのまま 力学的エネルギー保存の法則 になります。

つまり、重力による等加速度運動の問題では、
- エネルギー保存の法則で解いても
- 等加速度運動で解いても
実は同じことを行っている というわけです。
運動量との違い(距離積分 vs 時間積分)
- 運動エネルギー: $\displaystyle\frac{1}{2}mv^2$
- 運動量: $mv$
どちらも「力 $F$ が与えられた結果の速度」を使うのに、なぜ違う物理量があるのでしょうか?
運動エネルギーは「距離で積分」
$$W=\int F\,dx$$
運動量は「時間で積分」
$$I=\int F\,dt$$
両者の式変形比較

つまり、
- 距離で積分 → 仕事 → 運動エネルギー
- 時間で積分 → 力積 → 運動量
という違いがあるわけです。
どちらも力 $F$ が起源なのに違う量が出てくるのは少しモヤモヤしますが、
「そういうものだ」と理解するのが一番しっくりきます。
- 力と距離が大切な物理量があり、
それが仕事であり、
それは運動エネルギーを変化させる - 時間が大切な物理量があり、
それが力積であり、
それは運動量を変化させる
ということで、その両者は
- エネルギー保存の法則、や
- 運動量保存の法則
といった独自の法則を持つ、ということです。
まとめ
この記事では、
- 1/2 が出る理由
- $v^2$ が出る理由
- 運動量との違い
を、できるだけ直感的に整理しました。
1/2 が出る理由
$v–t$ グラフが三角形になるから。

$v^2$ が出る理由
仕事は距離に比例し、距離は時間の2乗に比例するから。

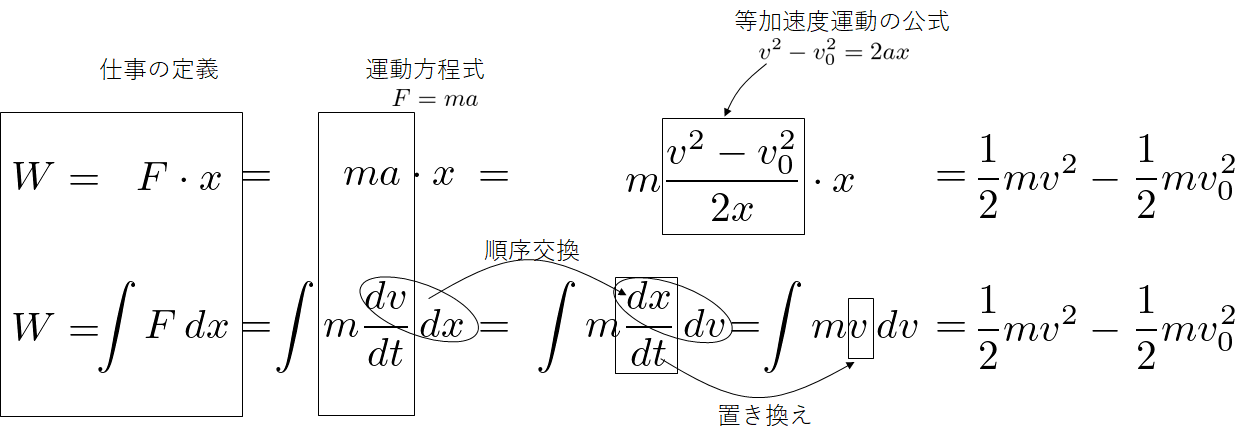
最後に、式変形をまとめるとこうなります。

この式変形を下記ページではより詳しく述べています:


コメント