微分を習い始めたとき、多くの人が「微分って何のために使うの?」と感じます。本記事では、微分の本質である「高次のグラフを書くための道具」という視点を、動画と図を使って“感覚レベルで理解できる”ように解説します。
さらに、かっこのままで微分する裏技や、導関数の線形性のイメージも紹介し、微分の計算と意味が一気にクリアになります。
微分は何のため?→高次のグラフを書くため
例題:$y=x^3-3x+1$ のグラフを微分で描く
次の問題を考えます。
$y=x^3-3x+1$ のグラフを書け。
微分でグラフの形が分かる仕組み(導関数の意味)
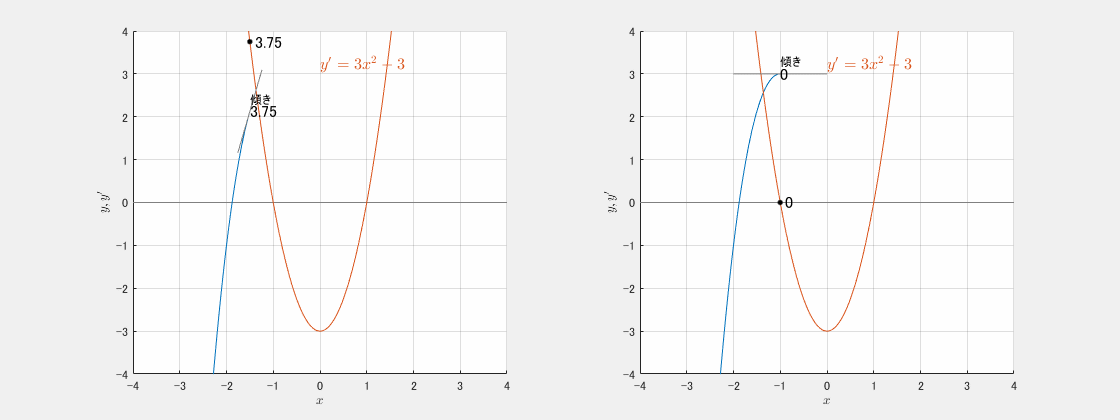
微分は「接線の傾き」=「超拡大したときのグラフの傾き」を表します。微分すると、
- $y^{\prime}=3x^2-3$
となります。この値は、元の関数 $y=x^3-3x+1$ の各点での傾きを表します。
【動画の見どころ】
- 導関数の値(赤)が元の関数の傾き(青に接している灰)として現れているところ
- 青と赤のグラフの対応関係
- 特に、青のグラフの傾きがゼロになるときの赤のグラフの値
適当な $x$ で止めて考えます(下図)。

赤のグラフが導関数で、その値が青のグラフの傾きになっています。
特に重要なのは、
導関数がゼロ $\iff$ 傾きがゼロ
という関係です。
導関数だけでは元のグラフの位置が決まらない理由
「増減の様子は分かるけれど、上下位置は不定では?」という疑問は鋭いです。
導関数は “傾きの情報” しか持たないため、上下位置関係は決まりません。
動画では $x=0$ のとき $y=1$ という1点の情報を使って位置を決めています。
微分情報だけでは不定になる理由(1点の情報が必要)
微分式 $y^{\prime}$ だけでは元の関数 $y$ は不定です。位置を決めるには元の関数が通る1点の情報が必要です。
2025年度の共通テストにも類題が出ています。(第3問:微分積分)
かっこのままで微分する裏技(平行移動のイメージ)
ここでは、次の式を楽に微分することを目指します。
- $y=(x-1)^5$
まず簡単な例として
- $y = (x-1)^2$
を使って、「展開して微分」と「かっこのまま微分」の両方を比較します。さらに、
- $y=(2x-1)^2$
も扱います。
より一般的な説明は以下の記事で扱っています:
該当箇所に直接ジャンプ→$y=(2x-1)^2$ の微分 かっこのままで微分する
まずは基本: $y=(x-1)^2$ を展開して微分する方法
展開すると、
- $y=x^2-2x+1$
微分して、
- $y^{\prime}=2x-2$
平行移動のイメージで “かっこのままで微分” する方法

赤:$y=(x-1)^2$
青:$y=x^2$
赤は青を右に1だけ平行移動したものです。だから、
$y=(x-1)^2$ を $x=2$ で微分した値 $=$ $y=x^2$ を $x=1$ で微分した値
となります。つまり、
$y^{\prime}=2(x-1)$
展開して求めたものと一致します。
【ここまでのまとめ】
- $(x-1)^2$ は $x^2$ を右に $1$ 平行移動しただけ
- だから微分も「右に $1$ ずらす」だけでよい
- 展開しても同じ結果になる
係数が $ 1$ でない場合の微分:$y=(2x-1)^2$ の扱い方
式変形すると、
$$y=4\left(x-\displaystyle\frac{1}{2}\right)^2$$
これは、$y=4x^2$ を右に $\displaystyle\frac{1}{2}$ 平行移動したものです。したがって、
$$y^{\prime}=4\cdot2\left(x-\displaystyle\frac{1}{2}\right)$$
展開して微分しても一致します。
高次の式も展開不要:$y=(x-1)^5$ の微分
高次になると展開は大変です。しかし、
$y=x^5$ の微分は $y^\prime=5x^4$
そして、$y=(x-1)^5$ は右に1平行移動しただけなので、
$$y^{\prime} = 5(x-1)^4$$
となります。
【ここまでのポイント】
- 平行移動のイメージで微分できる
- 係数が $1$ でない場合は式変形で対応
- 展開より圧倒的に速い
さらに詳しくは↓の記事で取り上げています。ここでは微分の連鎖律をイメージで理解することを目的にしています。
導関数の線形性は「超拡大したら直線」から自然に理解できる
微分には線形性があります。
- $y=kf(x)\Rightarrow y^{\prime}=kf^{\prime}(x)$
- $y=f(x)\pm g(x)\Rightarrow y^{\prime}=f^{\prime}(x)\pm g^{\prime}(x)$
これは、
曲線も超拡大したら直線になる
という微分の本質から自然に理解できます。
定数倍の微分:$y=kf(x)\Rightarrow y^{\prime}=kf^{\prime}(x)$
例:
- $k = 3$
- $f(x) = x^2$
つまり、
- $y = 3x^2$
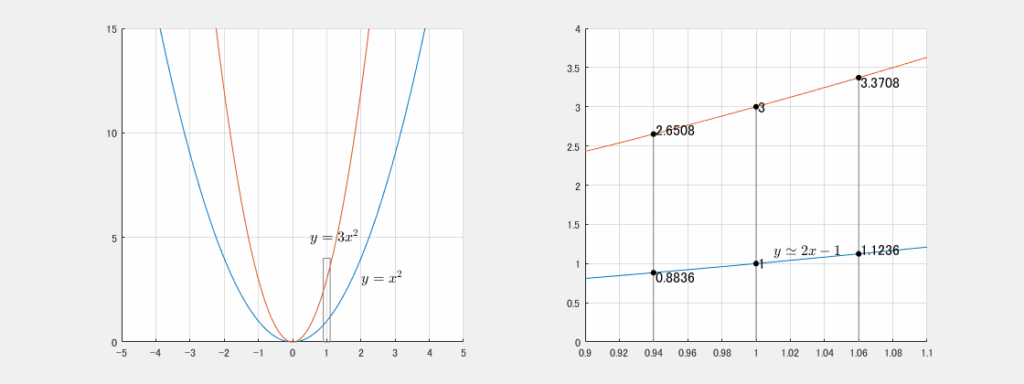
赤のグラフは青の3倍。だから傾きも3倍。
和の微分:$y=f(x)\pm g(x)\Rightarrow y^{\prime}=f^{\prime}(x)\pm g^{\prime}(x)$
例:
- $f(x) = x^2$
- $g(x) = x$
和は
- $y = x^2+x$

黄色のグラフは青と赤の和。だから傾きも和になる。
まとめ:微分の意味と計算が一気にクリアになる
【まとめ】
- 微分は「高次のグラフを書くための道具」
- 導関数は元の関数の傾きを表す
- 導関数だけでは上下位置は決まらない(1点の情報が必要)
- かっこのままで微分する裏技は「平行移動のイメージ」
- 導関数には線形性があり、超拡大すると直線になるという本質から自然に理解できる
これらを押さえると、微分の計算と意味が一気にクリアになります。
微分のイメージがつかめたら、次は「合成関数の微分(連鎖律)」をへ進むと理解が完成します。
→ 合成関数の微分(連鎖律のイメージ)
さらに、微分の応用問題を解いてみましょう。
→ 微分のイメージ増強演習




コメント