ベクトルの最大の魅力は、図形の関係をすべて計算で扱えるようにしてくれるところです。ひらめきや特殊な発想に頼らず、道具としてのベクトルを正しく使えば、図形問題は驚くほど整理されます。
この記事では、直線上の点・平行・垂直・角度・大きさ・三角形の面積といった図形の基本要素を、ベクトルという道具でどのように扱うのかを整理し、ベクトルの全体像を一望できるようにします。
直線上の点問題
使う道具
「点が直線上にある」と来たらこの道具を持ち出します。

$\overrightarrow{\mathrm{OP}} = t\,\overrightarrow{\mathrm{OA}} + (1-t)\,\overrightarrow{\mathrm{OB}}$
点 $\mathrm{P}$ が点 $\mathrm{A}$ と $\mathrm{B}$ を通る直線上にあるとき、
$$\overrightarrow{\mathrm{OP}} = t\,\overrightarrow{\mathrm{OA}} + (1-t)\,\overrightarrow{\mathrm{OB}} \tag{1}$$
と表せます。これは、座標平面で考えると自然に理解できます。

左図のように、任意の点 $\mathrm{P}$ は
$$\overrightarrow{\mathrm{OP}} = x\,\overrightarrow{\mathrm{OA}} + y\,\overrightarrow{\mathrm{OB}}$$
と表されます。さらに「点 $\mathrm{A}$ と点 $\mathrm{B}$ を通る直線」という条件は、
$$x+y=1$$
という制限を与えるので、式(1) が得られます。右図のように $\overrightarrow{\mathrm{OA}}$ と $\overrightarrow{\mathrm{OB}}$ が斜めでも同じです。
どちらが $t$ でどちらが $1-t$?:具体例で判断する
式(1) の形は分かっても、
- $t:1-t$ に内分?
- $1-t:t$ に内分?
と迷うことがあります。私の場合は、$t=0$ と $t=1$ を代入して判断します。
$t=0$ を代入すると $\overrightarrow{\mathrm{OP}} = t\,\overrightarrow{\mathrm{OA}} + (1-t)\,\overrightarrow{\mathrm{OB}}$ は、
$$\overrightarrow{\mathrm{OP}}=\overrightarrow{\mathrm{OB}}$$
となるので、点 $\mathrm{P}$ は点 $\mathrm{B}$ に一致します。よって下図の右側が正しいことが分かります。

参考記事
この式を深堀した記事があります:
$\overrightarrow{\mathrm{AP}} = k\overrightarrow{\mathrm{AB}}$:始点がそろうときの表現
始点がそろっている場合は、こちらの表現が便利です。
点 $\mathrm{P}$ が直線 $\mathrm{AB}$ 上にあるとき $\mathrm{P}$ の座標を求めよ。

直線上にあれば $\overrightarrow{\mathrm{AP}} = k\,\overrightarrow{\mathrm{AB}}$ が成り立ちます。
$$\begin{pmatrix}p-1\\p\end{pmatrix} = k\begin{pmatrix}2\\4\end{pmatrix}$$
から $k$, $p$ を求めれば、
$$k=\displaystyle\frac{1}{2},\; p=2$$
$$\therefore\mathrm{P}(2,3)$$
と求まります。
平行問題
使う道具:ペケ・イコール・ポン
平行ベクトルでは対応成分が比例します。このときの計算を私は「ペケ・イコール・ポン」と呼んでいます。

例題
これを使うと、$k$ を介さずに一気に求められます。先ほどの問題を平行問題の道具で解くと、
$$\begin{pmatrix}p-1\\p\end{pmatrix} /\! / \begin{pmatrix}1\\2\end{pmatrix}$$
なので、
$$2(p-1)=p$$
$$\therefore\; p=2$$
と、$k$ を介さずにすぐに求まります。
垂直問題
使う道具:内積=0
垂直問題を扱う道具は、内積=0。

例題
$\triangle\mathrm{PAB}=90^\circ$ のとき $\mathrm{P}$ の座標を求めよ。

垂直なので、
$$\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AP}}=0$$
\begin{eqnarray}
\begin{array}{c}
\begin{pmatrix}1\\2\end{pmatrix}\cdot\begin{pmatrix}p-1\\p\end{pmatrix}=0\\
(p-1)+2p=0\\
\therefore\; p=\displaystyle\frac{1}{3}
\end{array}
\end{eqnarray}
よって、
$$\mathrm{P}\left(\displaystyle\frac{1}{3},\,\displaystyle\frac{4}{3}\right)$$
角度問題
使う道具:内積の定義式
角度問題を扱う道具は、内積の定義式。

例題
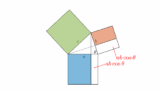
角度 $\theta$ を求めよ。

\begin{eqnarray}
\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}} &=& |\overrightarrow{\mathrm{OA}}||\overrightarrow{\mathrm{OB}}|\cos\theta\\
\begin{pmatrix}1\\\sqrt{3}\end{pmatrix}\cdot\begin{pmatrix}\sqrt{3}\\1\end{pmatrix} &=& \left|\begin{pmatrix}1\\\sqrt{3}\end{pmatrix}\right|\left|\begin{pmatrix}\sqrt{3}\\1\end{pmatrix}\right|\cos\theta\\
2\sqrt{3} &=& 2\cdot 2\cdot\cos\theta\\
\cos\theta &=& \frac{\sqrt{3}}{2}\\
\therefore\;\theta &=& \frac{\pi}{6}
\end{eqnarray}
この問題の場合は図形的解釈でも $\theta=\displaystyle\frac{\pi}{6}$ が分かりますが、ベクトルを使うメリットはそのような図形的解釈を持ってこなくても解けることです。
大きさ問題
使う道具:2乗して展開
終点同士を結んだベクトルの大きさを求めるときには2乗して展開。余弦定理そのものが現れます。

例題
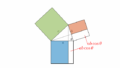
$\overrightarrow{\mathrm{AB}}$ の大きさを求めよ。

\begin{eqnarray}
|\overrightarrow{\mathrm{AB}}|^2 &=& |\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}|^2\\
&=& |\overrightarrow{\mathrm{OB}}|^2-2\times\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}}+|\overrightarrow{\mathrm{OA}}|^2\\
&=& 4-2\times 2\cdot 2\cdot\cos 30^\circ+4\\
&=& 8-4\sqrt{3}\\
&=& 2\,(\sqrt{3}-1)^2
\end{eqnarray}
ハタと気づきませんか?:余弦定理
余弦定理とは、三角形に対して成り立つ次の公式です。
$$\mathrm{AB}^2=\mathrm{OA}^2+\mathrm{OB}^2-2\cdot\mathrm{OA}\cdot\mathrm{OB}\cdot\cos\theta$$

これはまさに、上で求めた式そのものです。余弦定理については↓の記事でも詳しく扱っていて、↑はベクトル的視点から、↓は図形的視点から余弦定理をとらえています。
三角形の面積問題
使う道具:大きさの2乗と内積の2乗
三角形の面積は、底辺×高さ÷2をベクトルで表すだけです。公式を覚える必要はありません。計算すれば自然に導けます。

証明
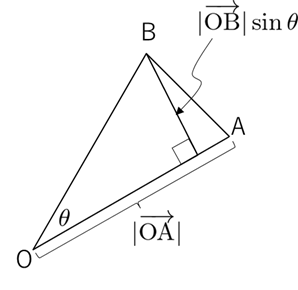
\begin{eqnarray}
S &=&\frac{1}{2} |\overrightarrow{\mathrm{OA}}||\overrightarrow{\mathrm{OB}}|\,\sin\theta\\
&=& \frac{1}{2} |\overrightarrow{\mathrm{OA}}||\overrightarrow{\mathrm{OB}}|\,\sqrt{1-\cos^2\theta}\\
&=& \frac{1}{2}\sqrt{|\overrightarrow{\mathrm{OA}}|^2|\overrightarrow{\mathrm{OB}}|^2-(\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}})^2}
\end{eqnarray}
$\theta=90^\circ$ からの類推も有効
$\theta=90^\circ$ のときは明らかに:
$$S = \frac{1}{2}|\overrightarrow{\mathrm{OA}}||\overrightarrow{\mathrm{OB}}|$$
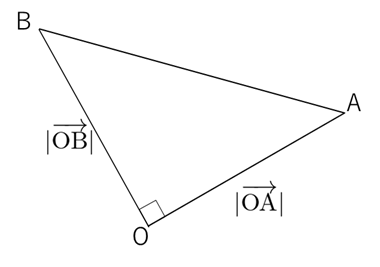
$\theta\ne 90^\circ$ のときはこの面積よりも小さくなるので、その補正項がつく、というイメージを持てばよいです。
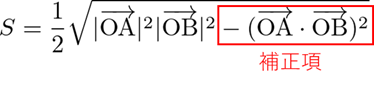
まとめ
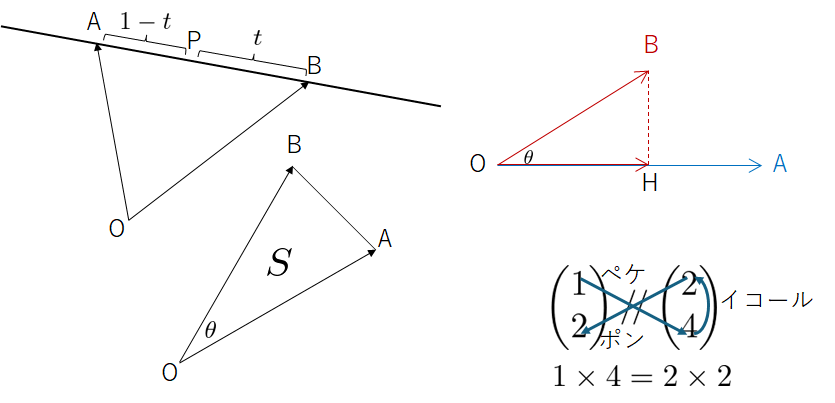
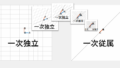
平面ベクトルの解法の全体像は、次の図のように整理できます。

ベクトルの利点は、図形的なひらめきがなくても計算で処理できるところです。計算量は増えますが、機械的にできる部分なので練習すれば必ず身につきます。


コメント