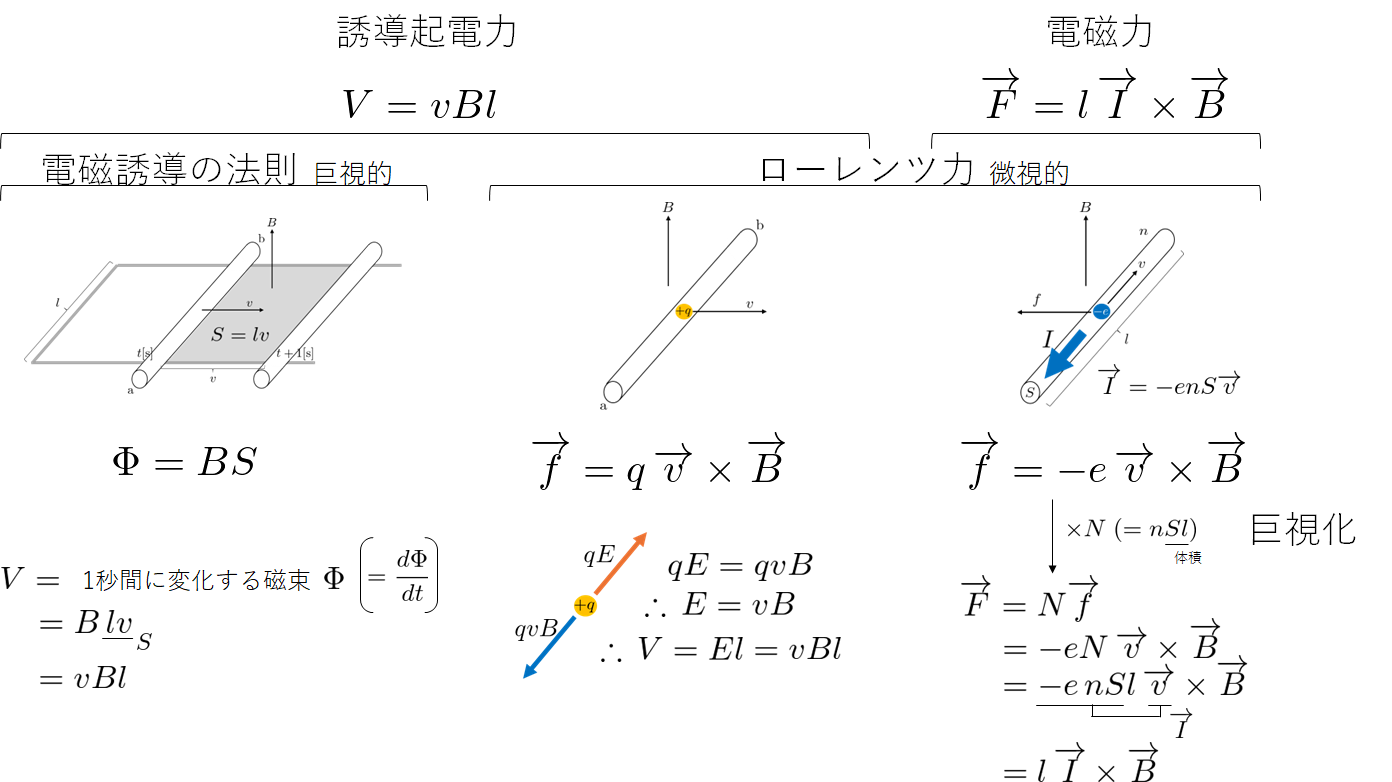
導体棒が磁場中を動くときに生じる誘導起電力 $V=vBl$ と、電流が流れる導体棒が受ける電磁力 $F=lIB$。これらは一見バラバラの公式に見えますが、実はどちらもローレンツ力から導出できるという共通の “芯” を持っています。
さらに、誘導起電力は電磁誘導の法則からも導出できます。この記事では、巨視的(電磁誘導)と微視的(ローレンツ力)の両面から導出し、全体像を一枚の絵として理解します。
これにより、電磁気で頻出の公式が“丸暗記”ではなく、本質から理解できるようになります。忘れても自力で導出できるようになるのが最大のメリットです。
導体棒の移動は、2025年共通テスト↓でも出題されました。
誘導起電力を電磁誘導の法則から導く(巨視的見方)
まずは巨視的な視点から、電磁誘導の法則
$V=\dfrac{d\Phi}{dt}$
を使って、誘導起電力 $V=vBl$ を導きます。
この絵↓を理解することがこの章の目的です。

電磁誘導の法則:磁束が変化すると起電力が生じる
コイルを貫く磁束 $\Phi$ が時間とともに変化するとき、
$V=-N\dfrac{d\Phi}{dt}$

負号は向きの情報なので、以後は大きさと向きを分けて考えます。
導体棒が動く → 面積が増える
導体棒が速度 $v$ で動くと、コイルの面積が 1 秒間に
$S = lv$
だけ増えます。

面積が増える → 磁束が増える:$\dfrac{d\Phi}{dt}=vBl$
磁場の強さが $B$ なので、1 秒間に増える磁束は
$\Phi =\,$$v$$\,B\,$$l$

磁束の増加はそのまま誘導起電力:$V=vBl$
よって、
$V=vBl$
が得られます。
より厳密には $S=lx$ として $V=\dfrac{d(BS)}{dt}=Bl\dfrac{dx}{dt}$ と書けますが、考え方は同じです。
誘導起電力をローレンツ力から導く(微視的見方)
次に、ローレンツ力
$f=qvB$
を使って、誘導起電力 $V=vBl$ を導きます。
この絵↓を理解することがこの章の目的です。

ローレンツ力が電荷を端に押し寄せる → 電場が生じる($E=vB$)
導体棒中の電子はローレンツ力 $f=\,$$qvB$ により端へ押しやられます。結果として、導体棒内部には電場 $E$ が生じます。

電子は押しやられ続けるわけではなく、ローレンツ力と電場による力がつり合ったところで止まります。
$qE =\,$$q$$vB$
$E =\,$$vB$
電位差は $V=El$ → $V=vBl$
電場が分かれば、導体棒の長さ $l$ を掛けるだけで電位差が求まります。
$V =\,$$E$$l\,=\,$$vB$$\,l$
電磁力をローレンツ力から導く(微視的見方)
最後に、ローレンツ力
$f=-evB$
を使って、電磁力 $F=lIB$ を導きます。
この絵↓を理解することがこの章の目的です。

電流の微視的表現:$\overrightarrow{I}=-enS\,\overrightarrow{v}$
電流とは「1秒間に通過する電荷量」です。電子密度 $n$、断面積 $S$、電子の速度 $v$ を使うと、
$I=\,$$-enS\,v$
電子1つのローレンツ力 → 導体棒全体の力へ
電子1つが受ける力は
$$f=-evB$$
導体棒に含まれる電子の個数は $N=nSl$ なので、総力は上記の $f$ にこの $N$ を掛けて、
$F = N\cdot f$
$=\,$$nS$$\;l\;\cdot\;\;($$-ev$$\;B)$
$= l\;$$I$$\;B$
まとめ:誘導起電力も電磁力も“ローレンツ力”で一本につながる
以上のように、
- 誘導起電力 $V=vBl$ は、巨視的(電磁誘導)と微視的(ローレンツ力)の両方から導ける
- 電磁力 $F=lIB$ は、電子が受けるローレンツ力の総和から導ける
というように、どちらの公式もローレンツ力を “芯” として統一的に理解できることが分かります。
この全体像がつかめていれば、公式を丸暗記する必要はありません。忘れても、基本の原理から自力で導出できます。電磁気の理解が一段深くなるはずです。




コメント