ヤングの実験は簡単に言えば【波の干渉:2次元】の遠方版です。そして回折格子はヤングの実験に対しては遠方かつ波源がたくさん版です。この違いだけで基本的には同じです。
【波の干渉:2次元】では腹と節が双曲線になることを述べましたが、十分遠方では双曲線は直線に近似できます。
問題設定の1と2が波長違いのヤングの実験、3が回折格子です。
シミュレーションでは簡単のため距離によらず振幅を一定としました。実際には広がる波では振幅は距離が離れれば小さくなりますが、そうするとかえって見づらくなるためです。
なお、【波の干渉:2次元】の記事はこちら↓です。
問題設定1_ヤングの実験:λ=2π, 波源間隔 d=6π で 波源の数 2, 同位相
腹(以下、明線)になる角度 θ1, θ2, ⋯ は? 十分遠方で測定するものとする。
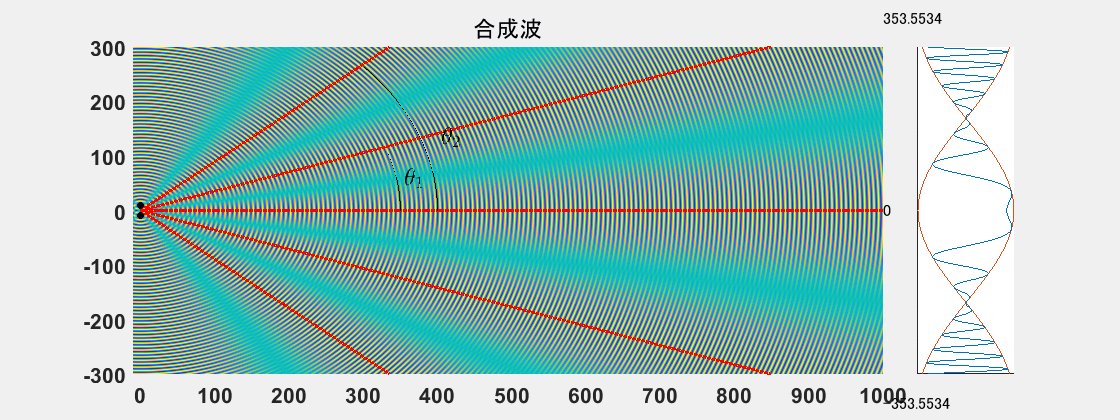
波源は A(−3π,0), B(3π,0) で 波長 λ=2π の波を同位相で出している。

この問題設定は#2と同じです。ただしこちらは十分遠方で測定しています。#2は近場での測定なので腹や節は双曲線ですが、十分遠方なら双曲線は直線っぽくなります。その角度を求めよ、というものです。
イメージ
注:実際には距離が離れれば振幅は小さくなりますが、ここでは見やすさを優先し一定としています。
解:dsinθn=nλ
明線になるのは図の光路差 dsinθn が波長の整数倍のときなので、

dsinθn=nλ
∴sinθn=nλd=n2π6π=n13
これを満たす θn のとき、明線となる。
解説1. 実際、何度?
sinθn=nλd
を満たす θn は解析的には求められません。三角関数表や計算機を使って出してみます。
sin19.5∘≒13sin41.8∘≒23sin90∘=33
なので、
θ1≒19.5∘θ2≒41.8∘θ3=90∘
であることが分かります。
解説2. スクリーン上の座標では?
このとき、L=1000 の地点にあるスクリーンでは、
x1=Ltanθ1≒353.5x2=Ltanθ2≒894.4
のところが明線になります。

問題設定2_ヤングの実験:λ=2π4, 波源間隔 d=6π で 波源の数 2, 同位相
波長が短くなると明線となる角度はどうなるでしょうか?
先の問題に対して波長を 14 にしてシミュレーションしてみます。
波長を短くするとは、相対的に波源間隔を広げることと同義です。ここの関係は興味深いので別投稿↓でイメージ強化を図ります。
イメージ
注:実際には距離が離れれば振幅は小さくなりますが、ここでは見やすさを優先し一定としています。
解:dsinθn=nλ
明線になるのは図の光路差 dsinθn が波長の整数倍のときなので、

dsinθn=nλ
∴sinθn=nλd=n2π46π=n112
これを満たす θn のとき、明線となる。
解説1. 実際、何度?
sin4.78∘≒112sin9.59∘≒212sin14.48∘≒312
なので、
θ1≒4.78∘θ2≒9.59∘θ3≒14.48∘
であることが分かります。
この場合は n=12 まで明線が計算できます。
解説2. スクリーン上の座標は?
このとき、L=1000 の地点にあるスクリーンでは、
x1=Ltanθ1≒83.6x2=Ltanθ2≒169.0x3=Ltanθ3≒258.2
のところが明線になります。

明線の間隔は、
x1–x0=83.6−0=83.6x2–x1=169.0−83.6=85.4x3–x2=258.2−169.0=89.2
とほぼ同じ間隔になっています。このことについては解説3で詳しく見ます。
解説3. 明線間隔はほぼ等間隔 sinθ≒θ≒tanθ により
角度 θ が小さい場合、明線の間隔はほとんど等間隔になります。式で表現するには、θ の単位を [rad] にして、
sinθ≒θ≒tanθ
を利用します。この関係は次のグラフから理解できます。3つの線が θ=0 付近ではほぼ重なっているということです。

グラフより、|θ|≤0.2[rad] くらいでは sinθ≒θ≒tanθ と言ってよさそうです。
ちなみに、θ=0.2[rad] は約 11.46∘ です。
このとき明線の位置は、
sinθn=nλdxn=Ltanθn
なので、sinθ≒θ≒tanθ を使うと、
xn=Ltanθn≒Lsinθn=L⋅nλd∴Δx=xn+1−xn≒L⋅λd=103⋅2π46π≒83.3
となります。
このように考えると幾分楽
上記の式変形は直接下記のように立式すると幾分楽になります。
dxnL≒nλ

問題設定3_回折格子:λ=2π4, 波源間隔(格子定数) d=6π で 波源多数, 同位相
波源の数が増えると何が変わるでしょうか?結論は、
明線の角度は同じで、明線強度がピーキーになる
です。その様子をシミュレーションで確認します。
なお、回折格子の場合、波源間隔は格子定数と呼ばれます。
イメージ
波源の数を 2, 10, 200 に変化させます。
波源の数が2のものは「問題設定2」と同じでヤングの実験ですが、波源の数を増やしていくとどうなるかを分かりやすくするためにここでも再掲します。ただし、スクリーンの位置は L=106 と、「問題設定2」の L=103 に比べて桁違いに大きくしています。これは、波源の数が増えるとスクリーンはより遠くにする必要が出るためです。
比較の意味では「問題設定2」のシミュレーションでも同じ L=106 とした方が分かりやすいですが、計算量が非常に大きいため、手持ちのコンピュータでは無理でした。そこでここではスクリーン上に現れる波形だけを計算することで計算量を減らしています。
注:実際には距離が離れれば振幅は小さくなりますが、ここでは見やすさを優先し一定としています。
解説1. 明線の位置(角度)は全て同じ
注目したいのは、ヤングの実験でも回折格子でも、また回折格子の中でもスリットの数によらず明線の角度は同じであるということです。
それは、明線の角度を決める式は全て
dsinθn=nλ
で同じだからです((1), (2))。
解説2. 波源が増えるとピーキーになる
波源が増えるとピーキーになります。それは、強め合う(明線になる)角度はどの波源からでも同じですが(例えばN=2の明線の位置を見たとき、青と赤の山谷は一致している)、その角度から少しでもずれると様々な波源からの様々な位相差の波が重なり合い、その結果として平均的にはゼロに近くなるためです。
解説3. 通常の問題では光の波長で問われる
今回のシミュレーションではスクリーンの位置が x=106 と非常に大きいですが、この単位を [μm] と考えれば現実的な大きさになりいろいろ納得がいきます。そうすると各種定数は単位付きで次のようになります。
- スクリーンの位置:x=106[μm]=1[m]
- 波長:λ=2π4[μm]≒1.57[μm](=1570[nm]) (赤外線)
- 格子定数:d=6π[μm]=18.84[μm]
です。赤外線になってしまったので良くないですね。可視光線はおおよそ380nm-780nmです1ので、今回のシミュレーションで波長をさらに半分、格子定数も半分にしてシミュレーションをすればよかったです。そうすれば明線間隔は今回のシミュレーションと同じとなり、それは(3)より、
- 明線間隔:83.3×103[μm]=83.3[mm]
で明線が表れます。
解説4. 実際の実験(山形大学のHPより)
山形大学のHPに回折格子の実験課題が載っており、いい写真があったので引用します。
課題2 回折格子 (yamagata-u.ac.jp)
このページには、赤だけでなく緑と青の写真もあり、波長の違いで角度がどのように変わるかが確認できます。また、CDを回折格子に見立ててCDの溝の間隔を求める実験も紹介されていて興味深いです。
まとめ
#2では波源が2つで近場の観察の場合は腹や節は双曲線になること、そして本稿#3では遠方ではほぼ直線になること(ヤングの実験)、そして波源が増えれば腹の振幅(明線強度)はピーキーになること(回折格子)を見てきました。
そして直線と見なせる遠方では明線になる角度は
dsinθn=nλ
で求められ、
sinθn≒tanθn=xnL
より
dxnL≒nλ
∴xn≒L⋅nλd
となり、明線間隔 Δx は
Δx≒L⋅λd
となります。






コメント