複素数とは、実数だけでは表しきれない世界を広げてくれる、ちょっと魔法のような存在です。「数直線」ではなく「複素数平面」で考えることで、その本質が驚くほど明快になります。本記事ではまずはその基本として、複素数の加減乗除がどのように「複素数平面上での座標変換」として理解できるのかを、図や動画を使って直感的に掴んでいきます。
複素数と複素数平面
複素数とは?
複素数は
$$z = a + bi$$
という形で表され、$a,b$ は実数、$i$ は虚数単位です。これは平面上の座標 $(a,b)$ として捉えることができるため、図形的な視点が非常に有効になります。
複素数平面
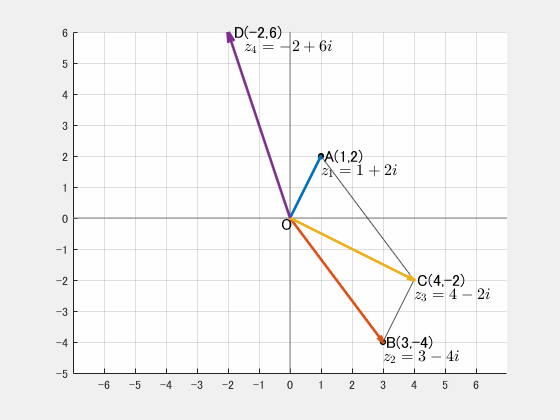
例えば、複素数 $z_1 = 1 + 2i$ は複素数平面上では $(1,2)$ に、$z_2 = 3 – 4i$ は $(3,-4)$ に対応させます。

座標変換としての加減乗除
加法と減法:ベクトルの和と差
複素数の加法・減法は、複素数平面上ではそのままベクトルの和と差として理解できます。
- 加法: $z_1 = 1 + 2i$, $z_2 = 3 – 4i$ のとき、
$$z_1 + z_2 = 4 – 2i$$
これは 2 つのベクトルを足した結果です。
- 減法:
$$z_1 – z_2 = -2 + 6i$$
こちらはベクトルの差に対応します。
乗法:回転と拡大
まずは簡単な例:$i$ を掛けると 90° 回転
複素数の掛け算は、複素平面上では回転+拡大という操作になります。まずは $i$ を掛ける例から見てみましょう。
- $i$ を掛けると?
$$(1 + i)\times i = -1 + i$$
これは点を90°反時計回りに回転させた結果です。
以下、ステップごとに確認していきます。
掛けられる数は $z_1 = 1 + i$、複素平面上では点 $\mathrm{A}(1,1)$ です。

掛ける数は $z_2 = i$、点 $\mathrm{B}(0,1)$。これは $x$ 軸から 90° の位置にあります。

実際に計算すると、
$$(1 + i)\times i = -1 + i$$
つまり $\mathrm{A}'(-1,1)$ です。

実際に 90° 回転させると、確かに $\mathrm{A}’$ に一致します。

一般的な例:60° 回転+拡大
次に、$z_1 = \sqrt{3} + i$ に $z_2 = 1 + \sqrt{3}i$ を掛ける例を見てみましょう。
$$(\sqrt{3}+i)(1+\sqrt{3}i)=4i$$
これを複素平面で表すと、以下の動画のようになります。
以下、ステップごとに確認します。
掛けられる数は $z_1 = \sqrt{3} + i$、点 $\mathrm{A}(\sqrt{3},1)$。

掛ける数 $z_2 = 1 + \sqrt{3}i$ は $x$ 軸から 60° の位置にあります(点 $\mathrm{B}(1,\sqrt{3})$)。

計算すると、
$$(\sqrt{3}+i)(1+\sqrt{3}i)=4i$$
つまり $\mathrm{A}'(0,4)$ です。

60° 回転させると角度は一致しますが、長さが異なります。

長さを 2 倍すると一致します。この「2」は掛ける数 $z_2$ の絶対値です。

このように、複素数の乗算は「回転」と「拡大」を同時に行う操作なのです。
三角関数の加法定理も複素数で一瞬
三角関数の加法定理は次の公式です。
$\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$
$\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$
実はこれも、複素数の乗法を使えば一瞬で証明できます。詳しくは以下の記事で解説しています。
除法:逆回転と縮小
除法は乗法の逆操作です。先ほどの例を逆にして考えてみましょう。
\begin{eqnarray} \frac{z_3}{z_2} &=& \frac{4i}{1+\sqrt{3}i} = \frac{4i(1-\sqrt{3}i)}{(1+\sqrt{3}i)(1-\sqrt{3}i)} \\ &=& \frac{4i+4\sqrt{3}}{4} = i+\sqrt{3} = \sqrt{3}+i \end{eqnarray}
つまり、$z_3$ は $z_2$ の角度(60°)だけ逆回転し、さらに $|z_2|=2$ で縮小されて元の $z_1$ に戻るわけです。
まとめ
複素数の演算は、複素数平面上の座標変換として統一的に理解できます。
✅ 加減 → ベクトルの和と差
✅ 乗算 → 回転+拡大
✅ 除算 → 逆回転+縮小
この視点を持つことで、複素数の世界が一気に直感的になります。ぜひ、実際に複素数をプロットして動かしてみてください。
複素数の計算が「平面の操作」として見えるようになると、次はその性質をもう少し深く知りたくなるはずです。これらの性質を図形的に整理した記事はこちらです。



コメント