方べきの定理はおそらく高校で習いますが、中学生でも理解できる内容です。使わなくても円周角の定理と相似を組み合わせれば解けるのですが、知っていれば楽に解けますし、また発想の引き出しにもなります。高校生は定期テスト用の基礎理解として活用ください。
2024年度の大学入試共通テストにはこの方べきの定理を使うような問題も出されています。記事にしていますので、最後のまとめのところにリンクを貼っておきます。
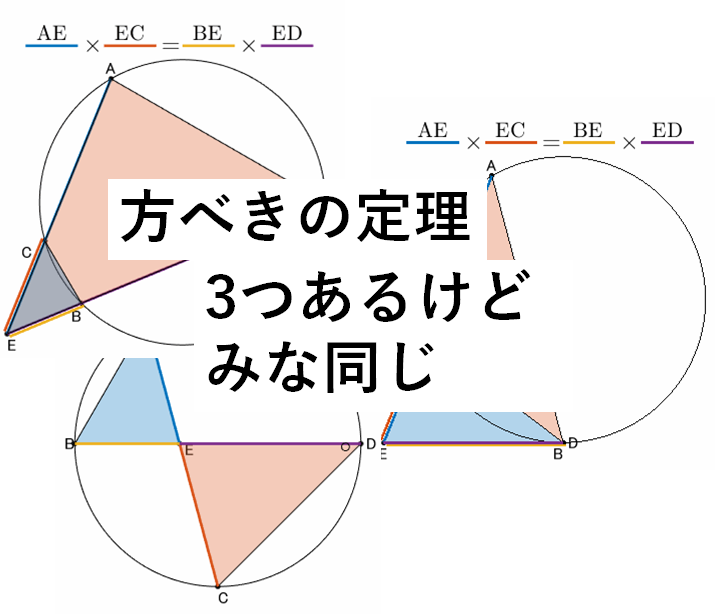
方べきの定理とは
3つの場合があり、それぞれ次のようです。
交点が円内の場合

交点が円外の場合

教科書とは表し方が少し異なるかもしれません。具体的には教科書では、
$$\mathrm{EC}\times\mathrm{EA}=\mathrm{EB}\times\mathrm{ED}$$
という順番かもしれません。覚えるときには教科書のように覚えた方が覚えやすいと思いますが、ここでは上記の「交点が円内の場合」との統一性を理解するためにあえてこの順番にしています。後に示す一連動画を見ると納得できます。
交点が円外でかつ一つが円の接線の場合

接線の交点が2つありますが、同じ点です。$\mathrm{B}=\mathrm{D}$ です。これも教科書では一つの点として扱いますが、ここではこれまでのものとの統一性を理解するためにあえて分けて書いています。
統一的に理解する
アニメーションで統一的に理解
上記の3つの公式を動画を用いて統一的に理解します。
ステップバイステップで確認します。
交点が円内の場合を証明
$$\triangle\mathrm{EAB}\unicode[sans-serif]{x223D}\triangle\mathrm{EDC}$$
の理解がキモです。それを見ていきます。そのために円周角の定理を用います。すなわち、

です。そして、対角は等しいので、
$$\angle\mathrm{AEB}=\angle\mathrm{DEC}$$
です。2角が等しいのでこの2つの三角形は相似です。実際、$\triangle\mathrm{EAB}$ を反転させてみると相似であることが直感的に理解できます。

相似が分かったので相似比を立てます。すなわち、
$$\mathrm{AE}:\mathrm{ED}=\mathrm{BE}:\mathrm{EC}$$
これを整理すると方べきの定理
$$\mathrm{AE}\times\mathrm{EC}=\mathrm{BE}\times\mathrm{ED}$$
が得られます。
円内にあれば左図であれ右図であれ、同じように方べきの定理は成り立ちます。


交点が円外の場合を証明
この場合の図を再掲します。

これも相似の証明がキモです。今度は
$$\triangle\mathrm{EAD}\unicode[sans-serif]{x223D}\triangle\mathrm{EBC}$$
の理解です。三角形が見やすいように色付けします。

四角形$\mathrm{ADBC}$ は円に内接しており、円に内接している対角の和は $180^\circ$ であることから、
$$\angle\mathrm{CAD}+\angle\mathrm{CBD}=180^\circ$$
一方、当然ながら一直線も $180^\circ$ なので
$$\angle\mathrm{CBE}+\angle\mathrm{CBD}=180^\circ$$
両式より、
$$\angle\mathrm{CAD}=\angle\mathrm{CBE}$$
となります。そして、$\angle\mathrm{E}$ は共通の角なので、2つの三角形は相似です。
これも、$\triangle\mathrm{EBC}$ を反転して直感的に確かめておきます。

交点が円外でかつ一つが円の接線の場合を証明
この場合の図を再掲します。

これも同様に相似を理解することがキモです。接弦定理を用います。
接弦定理より、$\angle\mathrm{EBC}=\angle\mathrm{A}$
$\angle\mathrm{E}$ は共通の角なので2つの三角形は相似です。
同様に反転させて直感的に理解します。

全ては同じことであると理解する
以上を踏まえ、今一度一気通貫アニメーションを見てみるとその統一性が良く理解できると思います。再掲します。
練習問題
交点が円内の場合

解

アニメーションで確認:反転相似
相似でも解けるようにしておく
方べきの定理は円周角の定理と相似の掛け合わせです。相似でも解けるようにしておくことで、方べきの定理が思いつかなかったときにも相似で解くことができますし、また相似で解こうとしてしまった際に方べきの定理を思い出せば計算量が節約できます。

このように相似を思い浮かべ、
$$\sqrt{6}:2\sqrt{3}=2:\mathrm{EC}$$
としても $\mathrm{EC}$ を求められます。
交点が円外でかつ一つが円の接線の場合

解



アニメーションで一気通貫の理解
まとめ
方べきの定理の公式は3種類あるように見えますが、ここまで見てきたようにこの3つは本質的には全く同じです。証明をしようとすれば、角度が同じことを示すために円周角の定理、内接四角形の性質、接弦定理という円と角度についての性質を少し使い分ける必要がありますが、共通性をよく理解して使っていくことが大事です。
高校入試の例:2025年度四天王寺高校(直接該当箇所へはこちら)
2024年度大阪星光学院(直接該当箇所へはこちら)
大学入試の例:2024年度大学入試共通テスト(直接該当箇所へはこちら)。


コメント