空間の直線の表し方(基礎編)では、 「基準点+$t$×方向ベクトル」 という直線の型を学びました。
また、2次元で t を消去する流れ(超基礎編)では、 $t$ が“位置を表すパラメータ” であることを確認しました。
さらに、内分点・外分点(応用編)では、 ベクトル方程式だけで位置が求まる という統一的な見方を体験しました。
この記事では、その流れをさらに発展させて、 直線と平面の交点をベクトル方程式で求める方法 を扱います。
空間の直線の表し方(基礎編):
2次元で $t$ を消去する流れ(超基礎編):
内分点・外分点(応用編):
1. ベクトル方程式で直線を表す
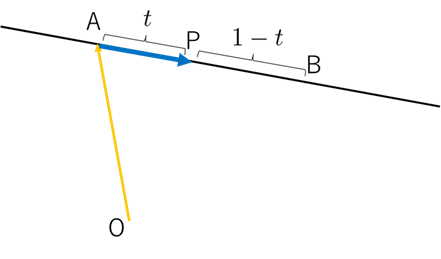
まずは、直線のベクトル方程式を復習しておきましょう。直線上の点は、
$$\overrightarrow{\mathrm{OP}}=\overrightarrow{\mathrm{OA}}+t\,\overrightarrow{\mathrm{AB}}$$
という形で表せます。ここで、
- $\overrightarrow{\mathrm{OA}}$:直線上の1点(基準点)
- $\overrightarrow{\mathrm{AB}}$:方向ベクトル
- $t$:実数(パラメータ)
2. 平面と直線の交点を求める
いよいよ本題です。直線のベクトル方程式を平面の式に代入し、パラメータ t を求めることで交点が求まります。
2-1. 例題
平面 $x+2y+2z=2$ と、
点 $\mathrm{P}(-2,-1,0)$ を通り、方向ベクトル $\begin{pmatrix}1\\1\\0\end{pmatrix}$ を持つ直線
との交点 $\mathrm{Q}$ を求めよ。
2-2. 直線をベクトル方程式で表す
直線上の点は「基準点+t×方向ベクトル」で表せるので、 その点が平面の式を満たす瞬間=交点 になります。
直線の式は、
$$\begin{pmatrix}x\\y\\z\end{pmatrix} =\begin{pmatrix}-2\\-1\\0\end{pmatrix} +t\begin{pmatrix}1\\1\\0\end{pmatrix}$$
成分で書くと、
\begin{eqnarray}
\left\{\begin{array}{l}
x &=& -2+t\\
y &=& -1+t\\
z &=&0
\end{array}\right.
\end{eqnarray}
2-3. 平面の式に代入する
平面の式 $x+2y+2z=2$ に代入すると、
$$(-2+t)+2(-1+t)+0=2$$
$$-2+t-2+2t=2$$
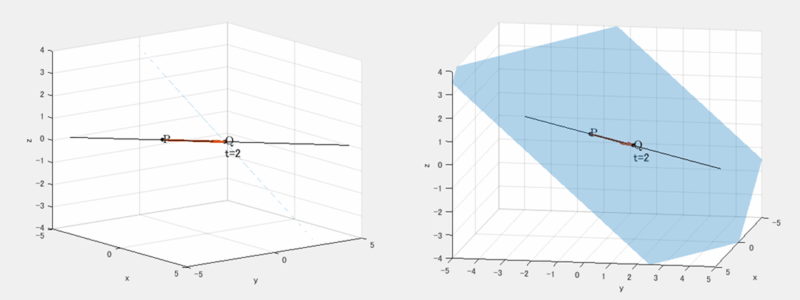
$$3t-4=2$$
$$t=2$$
ここで求めている t は、 点 $\mathrm{P}$ が平面に到達するまで、直線上をどれだけ進むか を表す量です。
2-4. 交点の座標を求める
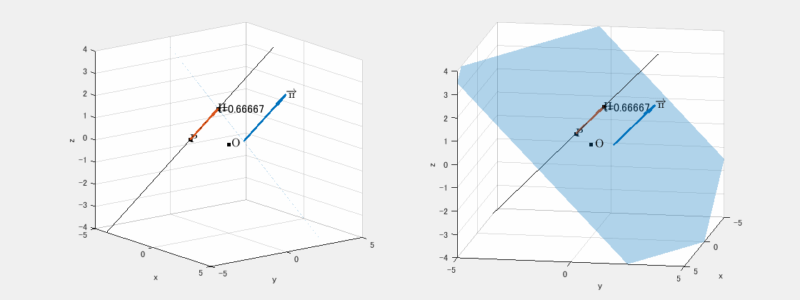
$$ \begin{pmatrix}x\\y\\z\end{pmatrix} = \begin{pmatrix}-2\\-1\\0\end{pmatrix} + 2\begin{pmatrix}1\\1\\0\end{pmatrix} = \begin{pmatrix}0\\1\\0\end{pmatrix} $$
よって交点は $\mathrm{Q}(0,1,0)$ です。
3. ベクトル方程式の応用:点と平面の距離にもつながる
今回見てきた平面と直線の交点を求める方法は、実は「点と平面の距離」を求めるときにも使われます。
点と平面の距離は、 点から平面に垂直に下ろした直線と平面の交点 を使って求めます。
つまり、今回扱った「交点を求める流れ」が、 そのまま距離の計算に直結します。
4. まとめ
- 直線は「基準点+$t$×方向ベクトル」で表せる
- 平面との交点は、直線の式を平面に代入して $t$ を求めるだけ
- 交点の計算は、点と平面の距離などの応用にもつながる
次の記事では、この交点の考え方を使って、 点と平面の距離を一瞬で求める方法 を見ていきます。







コメント