運動量保存の法則は「外力ゼロの運動方程式」｜積分による導出と力積の理解

　運動量保存の法則は2つの物体間に外力が働いていないという条件をうまく使って運動方程式を解いています。このおかげで、衝突のように相互作用の力が複雑で求めようのない場合でも扱うことができます。でも本質は「運動方程式を解いているだけ」です。そのことがよく分かる記事も書いていますので、あわせてご覧ください↓

運動量保存の法則

運動方程式を積分して導出

　運動量保存の法則は次の式です。

　これを導きます。出発点は運動方程式です。
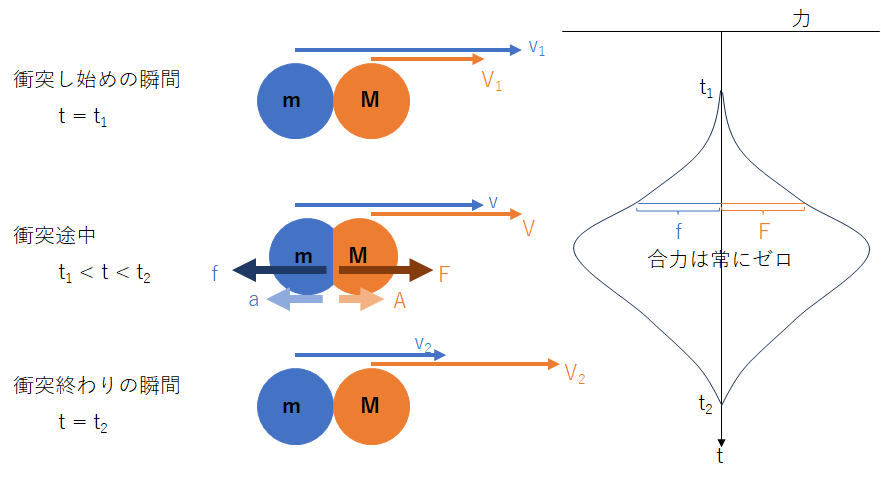
力が加わっているのは衝突している間だけなので、その時間だけに注目します。

まずは運動方程式を立てましょう。力を $f$, $F$、加速度を $a$, $A$ と置くと、
運動方程式は
\[ \left\{ \begin{array}{l} ma=f\\ MA=F \end{array} \right. \]
加速度は $a=\dfrac{dv}{dt}$ なので、次のように書けます。
\[ \left\{ \begin{array}{l} m\dfrac{dv}{dt}=f\tag{1}\label{p1194eq1}\\ M\dfrac{dV}{dt}=F \end{array} \right. \]

　ここで、衝突問題における重大な条件を使います。それは、

という事実です。これは作用反作用の法則です。式にすると
$$f+F=0$$
式\eqref{p1194eq1} の上下を足すと
$$m\dfrac{dv}{dt}+M\dfrac{dV}{dt}=0$$
となります。これを衝突時間 $t_1$ から $t_2$ まで積分します。

\begin{eqnarray}
左辺&=&m\displaystyle\int_{t_1}^{t_2}\displaystyle\frac{dv}{\cancel{dt}}\cancel{dt}+M\displaystyle\int_{t_1}^{t_2}\displaystyle\frac{dV}{\cancel{dt}}\cancel{dt}\\
&=&m\displaystyle\int_{v_1}^{v_2}dv+M\displaystyle\int_{V_1}^{V_2}dV\\
&=&m(v_2-v_1)+M(V_2-V_1)
\end{eqnarray}

右辺は 0 のままなので、整理すると
$$mv_1+MV_1=mv_2+MV_2$$

なんや！運動方程式そのものやん！！

　このように整理した後で運動量保存の法則を再び眺め返してみれば、なんや！運動方程式そのものやん！！と思いませんか？つまり、
$$mv_1+MV_1=mv_2+MV_2$$
を
$$m(v_2-v_1)+M(V_2-V_1)=0\tag{2}\label{p1194eq2}$$
に戻すことにより、
$$m\dfrac{dv}{dt}+M\dfrac{dV}{dt}=0$$
が見えてくれば、

外力ゼロの運動系における運動方程式を足し合わせただけ

だと再認識できます。

運動量保存のありがたいところ

　運動量保存のありがたいところは、衝突中にどんな力が働いているかを知る必要がないことです。衝突時間も知る必要がありません。これは衝突が相互作用だけで起きており、合力がゼロだからです。

　また、衝突時間は計測しづらいですが、積分してしまえば力が作用した結果としての速度の変化量が表に出てきます。速度は計測しやすい物理量なので、そこに置き換えられるのが非常にありがたいわけです。

力積について

力積の定義と運動量変化

　力 $f$ を時刻 $t_1$ から $t_2$ まで加えたとき、
$$\int_{t_1}^{t_2}f\,dt\tag{3}\label{eq3}$$
を力積と定義します。図で表すと下のグラフの面積です。

つまり、力積を受けたことで速度が $v_1$ から $v_2$ に変化した、ということです。
式\eqref{eq3} に運動方程式 $f=m\displaystyle\frac{dv}{dt}$ を入れて計算すると、

\begin{eqnarray}
\displaystyle\int_{t_1}^{t_2}f\, dt &=& \displaystyle\int_{t_1}^{t_2}m\displaystyle\frac{dv}{\cancel{dt}}\cancel{dt}\\
&=&m\displaystyle\int_{v_1}^{v_2}dv\\
&=&mv_2-mv_1
\end{eqnarray}

つまり、

与えた力積の量だけ運動量が変化する

ということです。

　青と橙の物体では力積の向きが逆で大きさが同じなので、運動量の変化量も逆向きで同じ。よって式\eqref{p1194eq2} が成り立ち、運動量保存となります。

スポーツの例

運動量の変化量から力を想像する：テニスラケット

　衝突によってどれほどの力が加わっているかを、運動量の変化から大まかに推定できます。力は本来時刻によって変化しますが、そこを「一定の力」とみなして考えます。つまり、下図のように青の部分を面積の等しい緑で置き換え、一定の力 $\bar{f}$ を考えるのです。

例えば、テニスのインパクトではどの程度の力が掛かっているのでしょうか。
記事を独立させました。続きはこちら↓をご覧ください。

まとめ

　運動量保存の法則を運動方程式から導きました。その際、「外力が働いていない」という条件を使いました。

　運動方程式は瞬間瞬間に成り立つ式ですが、衝突では「瞬間の振る舞い」ではなく結果に興味があるため、その間を積分で一気に飛ばしているわけです。

　導出過程を見ることで、公式が成り立つ条件（外力ゼロ）や注目点（結果の振る舞い）、そして「結局は運動方程式を解いているだけ」という安心感が得られます。

　実際、運動方程式を愚直に解いても同じ結果が得られます。その例は↓の記事にまとめています。