「この車は燃費がいい」とか「燃費のいい走り方はこうだ！」とか「カタログ値ほど実燃費は良くない」とか、ネットには燃費を題材にした記事がたくさんあります。
しかしながら燃費そのものを深堀して解説している記事はほとんどありません。
この記事では、長年自動車会社に勤め、中でもHV車の燃費向上制御技術開発に携わったことのある私が、「燃費とは何か」を高校物理の範囲で理解できるよう解説します。
この記事が分かるとこの後に続くシリーズの理解も容易になりますので、ぜひ最後まで読んでください。
燃費計算系の整理
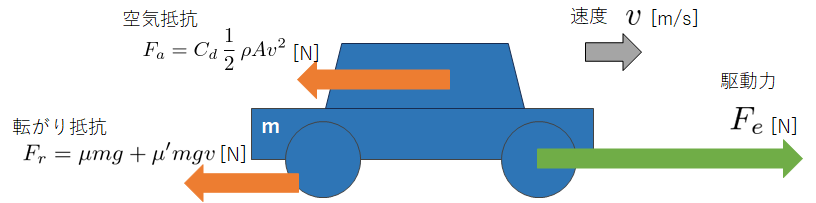
そもそも自動車が動くというのは、エンジンやモーターの力がタイヤに伝わり、走行抵抗に釣り合うことで実現されている物理現象です。
走行抵抗
走行抵抗とは自動車の進行方向とは逆向きに作用するすべての力を言い、次の4つから成ります。
- 転がり抵抗
- 空気抵抗
- 加速抵抗
- 勾配抵抗
転がり抵抗
転がり抵抗は理論的にはタイヤにかかる垂直抗力に比例します。しかし多くの実験により転がり抵抗は速度の1次に比例する項も有することが知られており、次の式で表されます。
$$F_{roll}=\mu mg+\mu^{\prime}mgv$$
空気抵抗
空気抵抗は車体の正面投影面積 $A$ と速度の2乗に比例し、次の式で表されます。
$$F_{air}=C_d\,\frac{1}{2}\,\rho A v^2$$
ここで、$C_d$ は空気抵抗係数、$\rho$ は空気密度です。
カタログなどで時々 $C_d$ 値などが謳われてますが、それはこれです。
加速抵抗
一般に、質量 $m$ のものが加速度 $a$ で加速するために必要な力 $F_{acc}$ は
$$F_{acc}=ma$$
です。これがまさに加速抵抗です。
ただし正確にはこの $m$ は車両質量と積み荷の質量だけではなく、内部のギヤ類が回転するのに要する慣性抵抗も含めて表現することにより、実際の質量よりも少し大きな値で設定します。
勾配抵抗
勾配抵抗は重力に逆らって坂道を上るのに要する力で、
$$F_{\theta}=mg\sin{\theta}$$
です。
しかしここでの燃費計算では簡単のため平坦な道路を走行するとし、勾配抵抗は考えないことにします。
走行抵抗のまとめ
以上から走行抵抗は次の式で表されます。
この式に、通常の小型乗用車を想定して具体的に $C_d$ や $A$ などの値を入れると例えば次のような式になります。
$$F_{all} = 0.05V^2+1.0V+100$$
ここで、$v$ の単位は $\mathrm{[m/s]}$、$V$ の単位は $\mathrm{[km/h]}$ です。
ここで重要なのは、
走行抵抗は速度の2乗に比例する項を有する
というところです。
エンジンのトルクと回転数
上記の駆動力 $F_e$ はもちろんエンジンが車軸を回転させる力（トルク）が源です。トルクが駆動力に変換される様子はグーネットのページに分かりやすい絵があったので引用します。
ギア比の計算方法と減速比の設定方法 | 車検や修理の情報満載グーネットピット (goo-net.com)
これを数式で表します。エンジンのトルクを $T_e\mathrm{[Nm]}$、トランスミッションのギヤ比を $i_M$、デフの減速比を $i_D$、タイヤの有効半径を $R\mathrm{[m]}$とすると、駆動力 $F_e\mathrm{[N]}$ は、
$$F_e=T_e\cdot i_M\cdot i_D\div R$$
$$\therefore\; T_e = \frac{F R}{i_D i_M}$$
です。
同様に、エンジンの回転数 $N_e\mathrm{[rpm]}$ はタイヤの回転数に対して $i_D\cdot i_M$ だけ速くなるので、
$$N_e = \frac{v}{2\pi R}\cdot 60\cdot i_D\cdot i_M$$
なお、これらの間には
$$P = Fv = 2\pi \frac{N_e}{60} T_e$$
の関係があります。駆動エネルギー $Fv$ はエンジンで発生するエネルギー $2\pi\displaystyle\frac{N_e}{60}T_e$ が源になっているので、当然です（損失が無いとした場合）。
エンジン燃費マップによる燃料消費量の計算
これまでの議論によりエンジン発生トルク $T_e$ と回転数 $N_e$ の計算ができるようになったので、この時の燃料消費量をエンジンマップより算出します。ここでは簡易的に下図のような等高線を持つエンジンマップを仮定します。
このエンジンは、$N_e=2700\mathrm{[rpm]}$, $T_e=65\mathrm{[Nm]}$ のときに燃料消費率 $f(N_e,\, T_e)=239\mathrm{[cc/sec]}$ にて最も燃費がよく、楕円状の等高線を持つとして、今回の燃費計算の実例のために私が適当に数式を作りました。
$$f(N_e,\, T_e) = \left(\frac{(N_e-2700)^2}{900^2}+\frac{(T_e-65)^2}{12.25^2}\right)^2+239$$
例えば、$N_e=3000\mathrm{[rpm]}$, $T_e=50\mathrm{[Nm]}$ の場合、$$\begin{eqnarray}
f(3000,\, 50) &=& \left(\frac{(3000-2700)^2}{900^2}+\frac{(50-65)^2}{12.25^2}\right)^2+239\\
&=& 241.6\mathrm{[cc/kWh]}\\
\end{eqnarray}$$
です。
このときのパワーは $P=2\pi \displaystyle\frac{N_e}{60} T_e\div 1000=15.71\mathrm{[kW]}$ なので、1秒間に消費される燃料 $E\mathrm{[cc/sec]}$ は、
$$E=241.6\times 15.71\div 3600=1.05\;\mathrm{[cc/sec]}$$
と計算できます。
燃費の計算
この計算を、走行するすべての時刻について実行し $E\mathrm{[cc/sec]}$ の総和を取れば燃料消費となります。
ただし、通常のエンジン車の場合、停車時でもアイドリングが生じています。アイドリング時の燃料消費量を $0.1083\mathrm{[cc/sec]}$ とすると1、燃料消費量がこの値に満たない場合とエンジン回転数が $1000\mathrm{[rpm]}$ に満たない場合にはアイドリングとしてこの値を燃料消費量とします。
ギヤ比を適切に選択した場合
ギヤ比を適切に選択した場合（ギヤ比を変えて上記の計算を施し、燃料消費量が最小になるギヤ比を最終的に選んだ）、その総和は $190.1\mathrm{[cc]}$ となりました。10$\cdot$15モードの走行距離は $4.16\mathrm{[km]}$ なので、燃費は
$$4.16\mathrm{[km]}\div 190.1\mathrm{[cc]} = 21.9\mathrm{[km/L]}$$
と計算できます。
この図の左側は走行中にエンジンマップ上のどこを利用できているかを示したものです。右側の下は速度とギヤを、上はパワーと $1$ 秒当たりの燃料消費量を表しています。
エンジンマップを見ると、比較的燃料消費効率の良い目玉辺りを多く使えているのが分かります。
ギヤを1速のままで走行した場合
ギヤを1速のままで走行した場合の燃費を考えます。この場合の燃料消費量の総和は $713.6\mathrm{[cc]}$ となりました。従って燃費は、
$$4.16\mathrm{[km]}\div 713.6\mathrm{[cc]} = 5.8\mathrm{[km/L]}$$
と計算できます。やはり相当燃費が悪いですね。
この場合は無駄に高回転領域を使っており、この部分は燃料消費効率が悪いために燃費が悪くなっていることが分かります。実際にこのような走行を行ってしまうとエンジンが壊れてしまう危険性すらありますが、ここはシミュレーションなのでその辺りは気にしないことにします。
ギヤを4速のままで走行した場合
ギヤを4速のままで走行した場合の燃費を考えます。この場合の燃料消費量の総和は $287.7\mathrm{[cc]}$ となりました。
従って燃費は、
$$4.16\mathrm{[km]}\div 287.7\mathrm{[cc]} = 14.5\mathrm{[km/L]}$$
と計算できます。やたら高速ギヤを使いすぎるのも燃費が悪くなります。
この時は逆に低回転領域ばかりを使い、燃費が悪くなっています。特に低回転で高トルクを生じる場合に大きな燃料消費量になっています。この場合は実際にはエンストを起こしてしまう可能性が高いです。
ギヤを適切に選ぶ意義
このようにギヤを適切に選ぶことは、走行に必要となるパワーに対してできるだけ燃料消費効率のよい目玉に近い部分を使うことができるために、燃費向上につながります。
このことを模式図で理解します(下図)。楕円の燃費曲線の上に反比例のグラフが書かれていますが、これは走行に必要なパワーを表しています。走行に必要なパワーをエンジンのトルクと回転数の積で得る訳ですが、この反比例のグラフはパワー一定の曲線であり、この中のどの点を使うかをギヤで選択します。この図の場合、3速を選ぶのが最も燃費がよい、ということになります。
CVTの場合はギヤ比が無段階（連続的に変化可能）であり、さらに目玉に近い部分を使うことができるために、燃費が向上します。下図にATとCVTの比較を模式図で示します。ATの場合でも上で見たようにギヤ段を選択することで省燃費化ができますが、離散的にしか選べないためベストではありません。それに対してCVTはギヤ段を連続的に選択できるため、ベストなギヤ段を選ぶことができます。
では、プリウスのようなHV車の場合はどうでしょうか？
プリウスのようなHV車の場合
プリウスにはエンジンのほかにモーターが搭載されている
プリウスの場合はさらに強力で、エンジンのほかにモーターを使用しています。モーターは駆動用と発電用の2つがあり、エンジンと合わせて3つの動力を巧みに操っています。これらは遊星歯車というギヤで連結されています。遊星歯車は下記のような太陽の周りを惑星が回る形をしたギヤです。
＜プリウス誕生秘話＞第2回 想定外の“ハイブリッド指令” （1994年12月～1995年8月） | トヨタ自動車のクルマ情報サイト‐GAZOO
プリウスの燃費が良い理由
そしてこれらを使ってどのように燃費を向上させているのかを、先ほどの模式図を使って理解してみます。ここでは簡単のため、モーターは発電も充電もひっくるめて1つで表現します。
通常のATやCVTの場合とは異なりプリウスにはモーターがついており、それが遊星歯車により連結されていることにより、エンジンの動作点を比較的自由に選ぶことができます。そこで、エンジンには一番効率のよい目玉の部分で運転しておいてもらい、走行に必要なパワーが小さい場合（図の左側）は、余分のパワーを発電機に振り分けることで充電に回し、反対に走行に必要なパワーが大きい場合（図の右側）は、不足のパワーを電池から補いモーターを回してアシストします。
そしてさらに、図の目玉の部分に一つ灰色部分が加わっていることに気づいたでしょうか。先ほどのエンジンに対し、特定の動作点ではあるけれどもさらに燃費が良くなるような改良を施しています。
さらにプリウスの場合は、停車時にはエンジンが止まっていること（アイドリングストップ）、またブレーキを踏んだ時にも走行の運動エネルギーで充電を行うこと（回生）により、さらに燃費が良くなります。
もちろん、実際の制御は上記ほど単純ではないですが、原理原則としてはこのようなことで燃費をよくしています。
まとめ
「燃費とは何か」を解説しました。燃費を計算するためには自動車に働く力を考える必要があり、それには次の4つがあることを述べました。
- 転がり抵抗
- 空気抵抗
- 加速抵抗
- 勾配抵抗
これらの和が車に働く走行抵抗であり、これらを元にして燃費を理解しました。
HV車はエンジンとモーターを組み合わせることにより、エンジンは常に効率の良いところを使い、要求パワーがそれより少ない時には余分なエンジンパワーは充電に回り、反対に足りない時にはモーターを駆動することにより、エンジンの効率を究極的に高めています。加えて回生により従来なら熱として捨てていたエネルギーを電気に戻すことで、さらに効率を高めています。
- 一般財団法人省エネルギーセンターのHPより、2000cc車で10分のアイドリング時に130ccの燃料消費量ということから。 ↩︎
コメント