入射波と反射波の合成波が進行しない波(定常波)になる様子をアニメーションで確認します。そしてそれを式変形でも確認します。
波の式自体は↓の記事で詳しく述べていますので合わせてみてください。
自由端反射と定常波
アニメーションイメージ
自由端反射は↓のアニメーションのイメージで、端点の x=5π でブランブランな状態で反射する場合です。青が進行波で赤が反射波として考えています。
入射波の式
入射波のグラフは青で、式は
y=sin(x−t)
です。というのも、t=0 のときの絵は

ですから、その青のグラフが
y=sinx
です。そして、T=2π でまた元の形に戻ります↓から、

y=sin(x−t)
です。なぜならこの式で t=2π とすれば、
y=sin(x−2π)=sinx
となり、確かに元に戻るからです。
波の式の導出については↓の記事で詳しく、だけどイメージ的に説明しています。
反射波の式
反射波のグラフは赤で式は
y=−sin(x+t)
です。というのも、t=0 のときの絵は

ですから、その赤のグラフが
y=−sinx
です。そして今度は逆向きに進むので、入射波の式で −t だった部分の符号を変えて +t にします。それで、
y=−sin(x+t)
となります。
合成波の式
合成波のグラフは紫(t>6π から登場)で式は
y=sin(x−t)−sin(x+t)
です。というのも、入射波の
y入=sin(x−t)
と、反射波の
y反=−sin(x+t)
の和だからです。下の絵は t=π/6 のときのものです。

- 入射波は青で、y=sin(x−π6)
- 反射波は赤で、y=−sin(x+π6)
- その和が紫で、y=−cosx
となっています。和の計算は、一般形で示すと(1)を三角関数の和積の公式を用いて
y=sin(x−t)−sin(x+t)=2cos(x−t)+(x+t)2sin(x−t)−(x+t)2=2cosxsin(−t)=−2cosxsint=−2sintcosx
となります。確かに、(2)の t に t=π/6 を入れると y=−cosx になっています。
合成波は上のアニメーションでも見たように進行しない波(定常波)ですが、式の上でも、
x と t がきれいに分離した
ことにより進行しない波を表現しています。このとき、
A=−2sint
は
時刻 t における振幅
を表します。
x と t がきれいに分離したことにより進行しない波を表現、について
この表現で「うんうん、そうだよね」と納得できた人は読み飛ばしてもらって大丈夫です。納得しきれなかった人は、具体的に t の値をいくつか定めてグラフを書いてみましょう。
t=0
このとき式(2)は
y=−2sin0×cosx=−2⋅0×cosx=0
です。

t=π/6
このとき式(2)は
y=−2sinπ6×cosx=−2⋅12×cosx=−cosx
です。

t の項 (sinπ6) は x の項 (cosx) とは切り離され、単なる振幅と化してしまっているため、波の形は cosx のままで振幅が調整されているだけです。
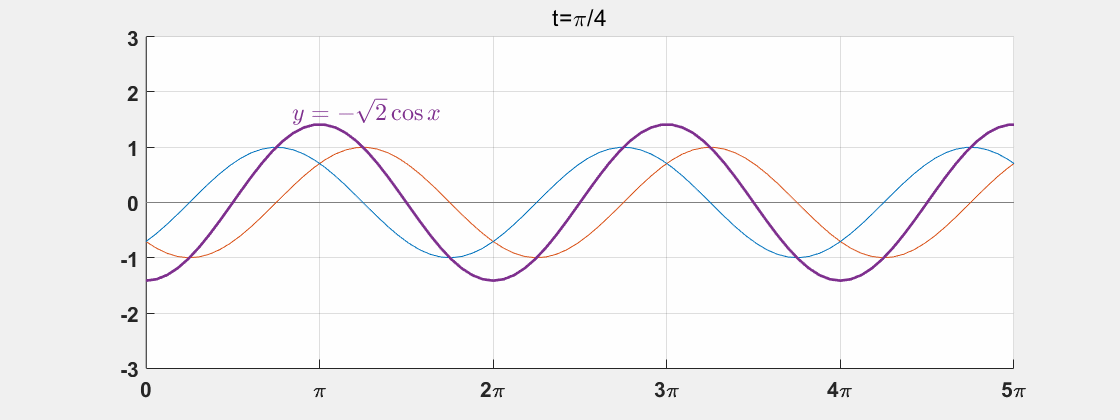
t=π/4
このとき式(2)は
y=−2sinπ4×cosx=−2⋅1√2×cosx=−√2cosx
です。

t の項 (sinπ4) は x の項 (cosx) とは切り離され、単なる振幅と化してしまっているため、波の形は cosx のままで振幅が調整されているだけです。
t=π/2
このとき式(2)は
y=−2sinπ2×cosx=−2⋅1×cosx=−2cosx
です。

t の項 (sinπ2) は x の項 (cosx) とは切り離され、単なる振幅と化してしまっているため、波の形は cosx のままで振幅が調整されているだけです。
t=π
このとき式(2)は
y=−2sinπ×cosx=−2⋅0×cosx=0
です。

t の項 (sinπ) は x の項 (cosx) とは切り離され、単なる振幅と化してしまっているため、波の形は cosx のままで振幅が調整されているだけです。
固定端反射と定常波
アニメーションイメージ
固定端反射は↓のアニメーションのイメージで、端点の x=5π で y=0 に固定された状態で反射する場合です。青が入射波で赤が反射波として考えています。
入射波の式
入射波のグラフは青で、式は
y=sin(x−t)
です。というのも、λ=2π, T=2π より、
y=sin(2πλx−2πTt)=sin(2π2πx−2π2πt)=sin(x−t)
だからです。
波の式の導出については↓の記事で説明しています。
反射波の式
反射波のグラフは赤で(t=0 では青と重なり見えていない)式は
y=sin(x+t)
です。というのも、t=0 のときのグラフの形は、アニメーションがイメージできれば
y=sinx
であることが分かり、入射波とは逆方向に動くので、t の符号を入射波のものと反対にしたもの(−t を +t にする)だからです。
反射による位相のずれについて
よく教科書では
固定端では端点での位相のずれは π
などと表現されます。このことと上記とを結びつけます。
まず、入射波は
y入=sin(x−t)
なので、端点 x=5π での振幅は
y入(x=5π)=sin(5π−t)=−sin(−t)=sint
です。これに対して反射波の位相のずれは π (すなわち位相は t→t+π)なので、この点での反射波 y反 は
y反(x=5π)=sin(t+π)=−sint
です。
確かにアニメーションでも y入 と y反 は反射点で逆の動きをしており、位相のずれは π とすることでそのことが表現できていることが分かります。
合成波の式
合成波のグラフは紫(t>6π から登場)で式は
y=sin(x−t)+sin(x+t)
です。というのも、入射波の
y入=sin(x−t)
と、反射波の
y反=sin(x+t)
の和だからです。
ここで、(3)を三角関数の和積の公式を用いて変形すると、
y=sin(x−t)+sin(x+t)=2sin(x−t)+(x+t)2cos(x−t)−(x+t)2=2sinxcos(−t)=2sinxcost=2costsinx
となります。
合成波は上のアニメーションでも見たように進行しない波(定常波)ですが、式の上でも、
x と t がきれいに分離した
ことにより進行しない波を表現しています。このとき、
A=2cost
は
時刻 t における振幅
を表します。
x と t がきれいに分離したことにより進行しない波を表現、について
この表現で「うんうん、そうだよね」と納得できた人は読み飛ばしてもらって大丈夫です。納得しきれなかった人は、具体的に t の値をいくつか定めてグラフを書いてみましょう。
t=0
このとき式(4)は
y=2cos0×sinx=2⋅1×sinx=2sinx
です。

t=π/6
このとき式(4)は
y=2cosπ6×sinx=2⋅√32×sinx=√3sinx
です。

t の項 (cosπ6) は x の項 (sinx) とは切り離され、単なる振幅と化してしまっているため、波の形は sinx のままで振幅が調整されているだけです。
t=π/4
このとき式(4)は
y=2cosπ4×sinx=2⋅1√2×sinx=√2sinx
です。

t の項 (cosπ4) は x の項 (sinx) とは切り離され、単なる振幅と化してしまっているため、波の形は sinx のままで振幅が調整されているだけです。
t=π/2
このとき式(4)は
y=2cosπ2×sinx=2⋅0×sinx=0
です。

t の項 (cosπ2) は x の項 (sinx) とは切り離され、単なる振幅と化してしまっているため、波の形は sinx のままで振幅が調整されているだけです。
t=π
このとき式(4)は
y=2cosπ×sinx=2⋅(−1)×sinx=−2sinx
です。

t の項 (cosπ) は x の項 (sinx) とは切り離され、単なる振幅と化してしまっているため、波の形は sinx のままで振幅が調整されているだけです。
まとめ
自由端と固定端のそれぞれでの反射波を考え、入射波との合成波を求めました。
反射波の反射点での位相は、自由端ではずれは無く、固定端では π だけずれますが、式を書く際には今回示したようなアニメーションがイメージできれば必ずしもそのことを意識せずとも自然にそのことが反映された式を書くことができます。
入射波と反射波とを重ね合わせた合成波は進行しない波となり、定常波と呼ばれます。式では x の項と t の項が分離した
y合=2costsinx
のような形となります。
このとき、定常波の時刻 t における振幅 A は
A=2cost
である、ということになります。





コメント