点と直線の距離には便利な公式がありますが、実はそれ以上に大事なのは「公式を忘れても楽に求められる」ことです。この記事では、過去の記事
- 【垂線の足】
- 【直線に関して対称な点】
で扱った「射影ベクトル」の考え方を使って、点と直線の距離を最速で求める方法を解説します。
内容的には一部重複しますが、公式を覚えようとして苦労している人をよく見かけるため、独立した記事としてまとめました。
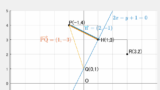
ここで射影ベクトルの意味がつかめれば、3次元版の【点と平面の距離】の公式も全く同じ発想で理解できます。
公式の確認と、ここで理解したい式
公式の確認
点と直線との距離には次の公式があります。
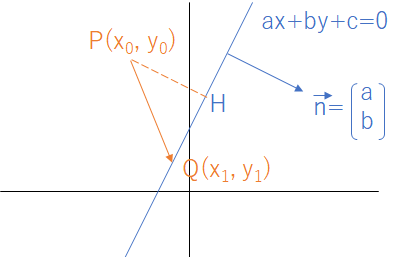
直線 $ax+by+c=0$ と点 $\mathrm{P}(x_0,y_0)$ との距離 $d$ は、
$$d=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}$$
ここで理解したい式:射影ベクトル
この記事で理解したいのは、次の「射影ベクトルによる距離」の式です。
$$d=\frac{|\overrightarrow{\mathrm{PQ}}\cdot\overrightarrow{n}|}{|\overrightarrow{n}|}$$
- $\mathrm{Q}$:直線上の任意の点(どこでもよい)
- $\overrightarrow{n}$:法線ベクトル
この式と公式が一致すれば、この記事の目的は達成です。
なお、分子の絶対値は鈍角の場合も含めて表現するためです。
公式で解く(比較のため)
まずは公式を使うとどうなるかを確認します。
直線 $y=2x+1$ と点 $\mathrm{P}(-1,4)$ との距離 $d$ を求めよ。
直線を $ax+by+c=0$ の形にすると
$$2x – y + 1 = 0$$
よって
$$\begin{eqnarray}
d &=& \frac{|2\cdot (-1)+(-1)\cdot 4+1|}{\sqrt{2^2+(-1)^2}}=\frac{5}{\sqrt{5}}\\
&=& \sqrt{5}
\end{eqnarray}$$
射影ベクトルで理解する距離(本命)
直線上の点を一つ選びます。扱いやすいので $\mathrm{Q}(0,1)$ とします。
(どこでもよい理由は後で説明します)
解
直線 $l:2x-y+1=0$ の法線ベクトルは、$\overrightarrow{n}=\begin{pmatrix}2\\-1\end{pmatrix}$。
点 $\mathrm{P}(-1,4)$ から直線 $l$ 上の点 $\mathrm{Q}(0,1)$ へのベクトルは、
$$\overrightarrow{\mathrm{PQ}}=\begin{pmatrix}1\\-3\end{pmatrix}$$
よって距離 $d$ は
\begin{eqnarray}
d &=& \frac{|\overrightarrow{\mathrm{PQ}}\cdot\overrightarrow{n}|}{|\overrightarrow{n}|}
= \frac{5}{\sqrt5}\\
&=& \sqrt5
\end{eqnarray}
解説(アニメーション → ステップ)
まずは全体の流れをアニメーションで確認します。
ここからステップ・バイ・ステップで見ていきます。
1. 図示
直線 $2x-y+1=0$ の法線ベクトルである、$\overrightarrow{n}=\begin{pmatrix}2\\-1\end{pmatrix}$ を青色ベクトルで、
点 $\mathrm{P}(-1,4)$、垂線の足 $\mathrm{H}$ を黒丸点で図示します。

2. 法線ベクトルの始点を $\mathrm{P}$ に合わせる
内積を取るときのイメージがつかみやすいように、
法線ベクトルの始点を $\mathrm{P}$ に移動します。

ここでは $\overrightarrow{n}$ と $\overrightarrow{\mathrm{PH}}$ がぴったり重なってしまっていますが、それはたまたまです。
3. 内積を取る
内積の定義より、鋭角の場合、
$$\overrightarrow{\mathrm{PQ}}\cdot\overrightarrow{n}=|\overrightarrow{\mathrm{PH}}||\overrightarrow{n}|$$
です。鈍角の場合も含めて表現すれば、
$$|\overrightarrow{\mathrm{PQ}}\cdot\overrightarrow{n}|=|\overrightarrow{\mathrm{PH}}||\overrightarrow{n}|\tag{1}\label{p1571eq1}$$
です。
直線上の点 $\mathrm{Q}$ はダミーであり直線上ならどこでもよいです。
直線上にあるため、内積を取ると $\mathrm{H}$ に“集約”されます。


参考記事:
4. 距離の式が完成
\eqref{p1571eq1} $|\overrightarrow{\mathrm{PQ}}\cdot\overrightarrow{n}| = |\overrightarrow{\mathrm{PH}}||\overrightarrow{n}|$ より
$$|\overrightarrow{\mathrm{PH}}| = \frac{|\overrightarrow{\mathrm{PQ}}\cdot\overrightarrow{n}|}{|\overrightarrow{n}|}$$
となり、距離の式が完成します

公式の証明(射影ベクトルから導く)
射影ベクトルの式が理解できれば、公式の証明は簡単です。
条件整理:
- 直線 $l:\;ax+by+c=0$
- 点 $\mathrm{P}:\;(x_0,y_0)$
- 法線ベクトル $\overrightarrow{n}=\begin{pmatrix}a\\b\end{pmatrix}$
- 直線上の点 $\mathrm{Q}:\;(x_1,y_1)$
$$\cdots\; ax_1+by_1+c=0\;\text{を満たす}\tag{2}\label{p1571eq2}$$
なので、
\begin{eqnarray}
d &=& \frac{|\overrightarrow{\mathrm{PQ}}\cdot\overrightarrow{n}|}{|\overrightarrow{n}|}\\
&=& \frac{|a(x_1-x_0)+b(y_1-y_0)|}{\sqrt{a^2+b^2}}\\
&=& \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}\quad(\because\eqref{p1571eq2})
\end{eqnarray}
ベクトル方程式で解く別解
直線 $l: 2x-y+1=0$ の法線ベクトルは、$\overrightarrow{n}=\begin{pmatrix}2\\-1\end{pmatrix}$。
点 $\mathrm{P}(-1,4)$ を通りこの方向に進む直線は、
$$\begin{pmatrix} x\\ y\end{pmatrix} = \begin{pmatrix} -1\\ 4\end{pmatrix} + t\begin{pmatrix} 2 \\ -1\end{pmatrix}$$
これが直線 $l$ と交わるのは $t=1$ のとき。
よって、
$$|\overrightarrow{\mathrm{PH}}| = |t\overrightarrow{n}| = \sqrt5$$
まとめ:状況別のおすすめ解法
公式は覚えていれば早くて便利ですが、中途半端だとミスにつながります。公式のイメージをしっかりと理解しておくことと、また公式を忘れても解けることが重要です。
公式も含め、他の手段の状況別おすすめ解法をまとめます。
| 状況 | 方法 | 理由 |
|---|---|---|
| 速く解きたい | 公式 | 計算が短い |
| 意味を理解したい | 射影ベクトル | イメージ的でミスが少ない |
| 応用したい | ベクトル方程式 | 3次元にも拡張しやすい |
3次元版はこちら:



コメント