軌跡問題の基本はパラメータ消去ですが、無邪気に消し去ってばかりいると落とし穴にハマるときがあります。無邪気さの中にも正確さを秘めて行動したいです。
落とし穴にハマるパラメータ消去問題の例
問題設定
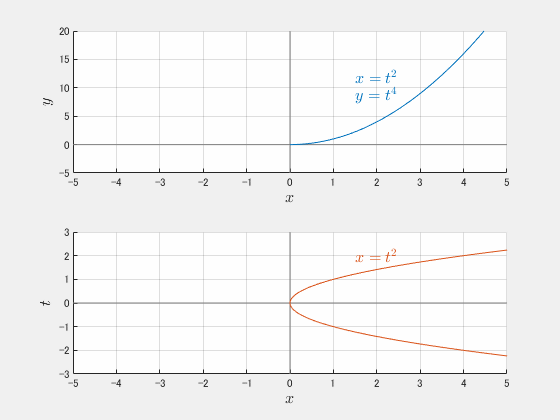
$t$ が実数全体を動くとき、点 $\mathrm{P}(t^2, t^4)$ の軌跡を求めよ。
$t$ を実数全体で変化させると実際にどうなるかを見た図が下記です。下の図が $t-x$ を表し、上の図が $x-y$ を表しています。
無邪気なパラメータ消去で間違った解答
間違った解
点 $\mathrm{P}$ の座標を $(x,y)$ と置くと、
\begin{eqnarray}
\left\{ \begin{array}{l}
x=t^2 \tag{1-1}\label{p2000eq1-1}\\
y=t^4
\end{array}
\right.
\end{eqnarray}
\eqref{p2000eq1-1}の上側の式を下側の式に代入して、
$$y=x^2\tag{1-2}\label{p2000eq1-2}$$
$x$ の取りうる範囲を意識する
$t$ の範囲は実数全体なので、$0$ も $1$ も $2$ も $-1$ も取りますが、一方 $x$ は正しか取りません。従って正しい解答は次のようになります。
正しい解
点 $\mathrm{P}$ の座標を $(x,y)$ と置くと、
\begin{eqnarray}
\left\{ \begin{array}{l}
x=t^2 \tag{2-1}\label{p2000eq2-1}\\
y=t^4
\end{array}
\right.
\end{eqnarray}
\eqref{p2000eq2-1}の上側の式を下側の式に代入して、
$$y=x^2\tag{2-2}\label{p2000eq2-2}$$
かつ、\eqref{p2000eq2-1}の上の式より
$$x\ge 0\tag{2-3}\label{p2000eq2-3}$$
よって、
$$y=x^2\;\;(x\ge 0)$$
同値変形をしなくてはならない：代入法の原理
[間違った解]と[正しい解]の違いは常に意識できるようにしておきましょう。無邪気にパラメータを消去しているだけでは時々落とし穴にハマります。
ポイントは、同値変形をしなくてはならない、ということです。[間違った解]の方でよくなかった点は、式\eqref{p2000eq1-1}の上側を下側に代入しただけで\eqref{p2000eq1-1}の上側を忘れ去ってしまっている点です。つまり、
\eqref{p2000eq1-1}の上側かつ\eqref{p2000eq1-1}の下側 を \eqref{p2000eq1-2}のみ
にしてしまった点です。同値にするためには代入元の方を残しておかなくてはなりません（代入法の原理）。つまり、
\eqref{p2000eq2-1}の上側かつ\eqref{p2000eq2-1}の下側 $\Leftrightarrow$ \eqref{p2000eq2-2}かつ\eqref{p2000eq2-3}
です。\eqref{p2000eq2-3}は代入元である\eqref{p2000eq2-1}のことです。
少しピンと来ていないかもしれないので、このことがよくわかる例を次に示します。
代入法の原理を理解する簡単な例
次の連立方程式を解け。
\begin{eqnarray}
\left\{ \begin{array}{l}
y=x+1\\
x^2+y^2=5
\end{array}
\right.
\end{eqnarray}
連立方程式の解はグラフの交点なので、下図のようになります。
間違った解
\begin{eqnarray}
\left\{ \begin{array}{l}
y=x+1 \tag{3-1}\label{p2000eq3-1}\\
x^2+y^2=5
\end{array}
\right.
\end{eqnarray}
\eqref{p2000eq3-1}の上の式を下の式に代入して、
$$x^2+(x+1)^2=5\tag{3-2}\label{p2000eq3-2}$$
これを整理すると、
$$(x+2)(x-1)=0$$
よって、
$$x=-2,\,1$$
これを\eqref{p2000eq3-1}の下側の式に代入する。
$x=-2$ のとき、
$$(-2)^2+y^2=5$$
$$y^2=1$$
$$\therefore y=\pm 1$$
$x=1$ のとき、
$$1^2+y^2=5$$
$$y^2=4$$
$$\therefore y=\pm 2$$
よって、
$$(x,y)=(-2,1),(-2,-1),(1,2),(1,-2)$$
正しい解
\begin{eqnarray}
\left\{ \begin{array}{l}
y=x+1 \tag{4-1}\label{p2000eq4-1}\\
x^2+y^2=5
\end{array}
\right.
\end{eqnarray}
\eqref{p2000eq4-1}の上の式を下の式に代入して、
$$x^2+(x+1)^2=5\tag{4-2}\label{p2000eq4-2}$$
これを整理すると、
$$(x+2)(x-1)=0$$
よって、
$$x=-2,\,1$$
これを\eqref{p2000eq4-1}の上側の式に代入する。
$x=-2$ のとき、
$$y=-2+1=-1$$
$x=1$ のとき、
$$y=1+1=2$$
よって、
$$(x,y)=(-2,-1),(1,2)$$
レビュー
さすがにこの問題に出会った際に[間違った解]のようには解かないと思いますが、なぜ皆さんがそうしないのかということを言語化して理解しておくことが重要です。それは、代入元は残しておかないと同値にならないから、です。数式で表現すれば、
[間違った解]：\eqref{p2000eq3-1}の上側かつ下側 $\Rightarrow$ \eqref{p2000eq3-2}かつ\eqref{p2000eq3-1}の下側
[正しい解]：\eqref{p2000eq4-1}の上側かつ下側 $\Leftrightarrow$ \eqref{p2000eq4-2}かつ\eqref{p2000eq4-1}の上側
です。[間違った解]の方では下側に代入したのち下側を使って解いていっており、代入元である上側が忘れられています。
【軌跡はパラメータを消去】の記事との関係性について
ここで、【軌跡はパラメータを消去】なぜこれで軌跡が求まるのかを完全理解との関係性を整理します。【軌跡はパラメータを消去】の記事では(i),(ii)と場合分けを行っており、これが同値性の意識です。つまり、式(1)を式(2)に代入して $m$ を消去して式(3)を得ていますが、代入元である式(1)もしっかり忘れておらず、式(1)の代わりに $x\ne 0$ としていること(i)と $x=0$ なら $y=0$ であること(ii)を使っています。
まとめ
軌跡や交点を求めたり、広く言えば連立方程式を解いたりする際には一方の式を他方に代入することにより文字消去を行います。このとき同値性を意識する重要性を述べました。
具体的には、代入元は残しておく、ということです。代入先の情報に加えて代入元の情報を残すことで、元の状態と同値な状態を保てます。
コメント