複素数平面の軌跡問題は、図形的な発想があるかどうかで難易度が大きく変わります。本記事では、2025年度の慶応・東大・早稲田の入試問題から、典型的な軌跡の型を整理しながら、図形的アプローチと計算的アプローチの両面から解説します。前回の記事(複素数平面の軌跡の基礎)を踏まえて読み進めると理解が一気に深まります。
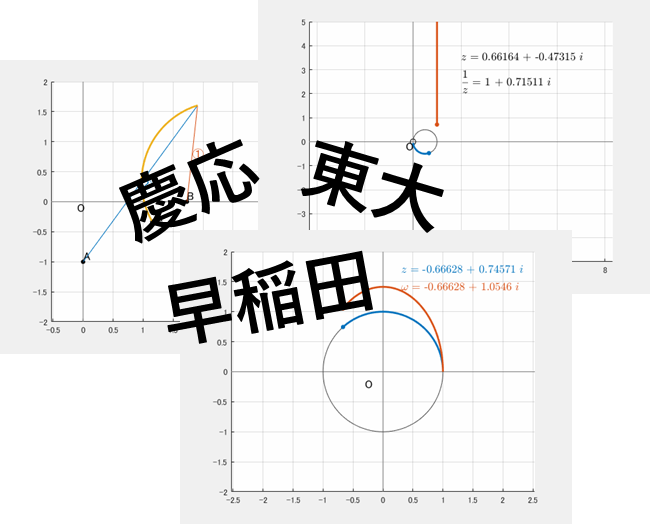
慶応義塾大学・理工学部:アポロニウスの円
複素数平面上で、方程式 $|z+i|=2|z-\sqrt{3}|$ を満たす点 $z$ 全体が表す図形は、中心が[ ]、半径が[ ]の円である。
解1:図形的に理解する(アポロニウスの円)
$$|z+i|:|z-\sqrt{3}|=2:1$$
これは、点 $\mathrm{A}(0,-1)$ と点 $\mathrm{B}(\sqrt{3},0)$ からの距離が $2:1$ である点の集合です。したがって、
内分点と外分点を直径の両端とする円(アポロニウスの円)
となります。具体的には、
内分点:$\mathrm{C}\left(\displaystyle\frac{2\sqrt{3}}{3},-\displaystyle\frac{1}{3}\right)$、外分点:$\mathrm{D}(2\sqrt{3},1)$
これらを直径とする円なので、
中心:$\left(\displaystyle\frac{4\sqrt{3}}{3},\displaystyle\frac{1}{3}\right)$
半径:$\displaystyle\frac{4}{3}$
解2:計算で求める
両辺を2乗して整理すると、
\begin{eqnarray}
(z+i)\overline{(z+i)} = 4(z-\sqrt{3})\overline{(z-\sqrt{3})}\\ 3z\overline{z}-4\sqrt{3}(z+\overline{z})+(z-\overline{z})i+11 = 0\\ \left|z-\left(\frac{4\sqrt{3}}{3}+\frac{1}{3}i\right)\right|^2 = \left(\frac{4}{3}\right)^2
\end{eqnarray}
よって、図形的アプローチと同じ円が得られます。
図形的理解のメリット
アポロニウスの円の型を知っていれば、計算をせずに一瞬で図形が分かります。基礎は前回の記事で整理しています。(アポロニウスの円の基礎はこちら)
東京大学:垂直二等分線
複素数平面上の点 $\displaystyle\frac{1}{2}$ を中心とする半径 $\displaystyle\frac{1}{2}$ の円の周から原点を除いた曲線を $C$ とする。
(1) 曲線 $C$ 上の複素数 $z$ に対し、$\displaystyle\frac{1}{z}$ の実部は $1$ であることを示せ。
(2)(3)は省略
解1:計算で示す
$z$ を次のようにおく:
$$z=\frac{1}{2}+\frac{1}{2}(\cos\theta+i\sin\theta)$$
これを用いて $\displaystyle\frac{1}{z}$ を計算すると、
\begin{eqnarray} \frac{1}{z} &=& 1-\frac{\sin\theta}{1+\cos\theta}i \end{eqnarray}
よって実部は $1$ です。
解2:図形的に理解する(垂直二等分線)
$C$ は
$$\left|z-\frac{1}{2}\right|=\frac{1}{2}$$
で表される円です。両辺を $\left|\displaystyle\frac{2}{z}\right|$ 倍すると、
$$\left|2-\frac{1}{z}\right|=\left|\frac{1}{z}\right|$$
これは、
点 $\displaystyle\frac{1}{z}$ が $(2,0)$ と $(0,0)$ の垂直二等分線上にある
ことを意味します。したがって実部は $1$ です。
複素数での垂直二等分線の基礎はこの記事で整理しています。(垂直二等分線の基礎はこちら)
早稲田大学:$|z|=1$ の扱い
複素数平面上で、複素数 $z$ が円 $|z|=1$ の上を動くとき、
$$\omega = \left(\frac{1+\sqrt{2}}{2}\right)z + \left(\frac{1-\sqrt{2}}{2}\right)\frac{1}{z}$$
を満たす点 $\omega$ の軌跡を求めよ。
解:三角関数表示で整理する
$|z|=1$ より、
$$z=\cos\theta+i\sin\theta$$
また、
$$\frac{1}{z}=\cos\theta-i\sin\theta$$
これらを代入すると、
\begin{eqnarray} \omega &=& \cos\theta+\sqrt{2}i\sin\theta \end{eqnarray}
よって、$\omega$ は楕円を描きます。
補足:$|z|=1$ の扱いのコツ
$|z|=1$ のときは、
$z\overline{z}=1$ から $z=\frac{1}{\displaystyle\overline{z}}$
または
$$z=\cos\theta+i\sin\theta$$
を使うのが基本です。逆数の扱いは前回の記事で整理しています。(逆数の性質はこちら)
まとめ
2025年度の入試問題から、複素数平面の軌跡の典型的な型を整理しました。図形的に理解できると計算よりもはるかに楽に本質が見えてきます。まずは基本の型を押さえ、必要に応じて計算でも確認できるようにしておくと、入試でも定期テストでも強力な武器になります。
軌跡の理解をさらに深めるには、複素数の逆数(反転)の性質を押さえておくと一気に視界が広がります。詳しくはこちらの記事で扱っています:






コメント