力学的エネルギー保存の法則は、
運動方程式を積分するだけで自然に導かれる ものです。
この記事では、次の3つのステップで理解を深めます。
- 運動方程式を積分してエネルギー保存則を導く
- 重力・ばね・万有引力・電位などの位置エネルギーを導出する
- 等加速度運動の公式とのつながりを理解する
特に、等加速度運動の公式
$$v^2 – v_0^2 = 2as$$
が エネルギー保存の法則と同じ式になる という事実は、
物理の世界が一本につながる瞬間です。
運動方程式を積分してエネルギー保存則を導く
運動方程式に $v$ を掛けて積分する
運動方程式
$$m\frac{dv}{dt} = F$$
の両辺に速度
$$v = \frac{dx}{dt}$$
を掛けて、時間で積分します。
$$\int_{t_1}^{t_2} m v\frac{dv}{dt}\,dt=\int_{t_1}^{t_2} F\frac{dx}{dt}\,dt$$
左辺と右辺を分けて計算すると、
左辺 $=\displaystyle\int_{v_1}^{v_2} mv\,dv=\frac12 mv_2^2 – \frac12 mv_1^2$
右辺 $=\displaystyle\int_{x_1}^{x_2} F\,dx = W$
ここで $W$ は外力がした仕事です。
したがって、
$$\frac12 mv_2^2 – \frac12 mv_1^2 = W$$
これは
「なされた仕事の分だけ運動エネルギーが増える」
という意味です。
関連:運動エネルギーの式の「1/2」はどこから来る?
仕事の定義に運動方程式を代入する(別の導出)
仕事の定義
$$W=\int F\,dx$$
に、運動方程式
$$F = m\frac{dv}{dt}$$
を代入しても同じ式が得られます。
\begin{eqnarray}
W &=& \int_{x_1}^{x_2} m\frac{dv}{dt}\,dx\\
&=& \int_{v_1}^{v_2} mv\,dv\\
&=& \frac12 mv_2^2 – \frac12 mv_1^2
\end{eqnarray}
式の途中で、
$$v=\frac{dx}{dt}$$
を代入しています。
これをパッと見で見やすく一行で表すと下記のようです。見やすさのため、積分区間の下端と上端は省略します。

様々な力による位置エネルギーを導く
重力の位置エネルギー:重力がした仕事ととらえる
重力は $F=-mg$。

高さ $h$ から 0 まで落下するとき、重力がした仕事は
$$W=\int_h^0 (-mg)\,dx = mgh$$
したがって、
$$\frac12 mv_2^2 – \frac12 mv_1^2 = mgh\tag{1}\label{p1244eq1}$$
この $mgh$ を 位置エネルギー(ポテンシャルエネルギー) と呼びます。
重力の位置エネルギー: $mgh$
等加速度運動の公式と同じ式になる
この式\eqref{p1244eq1}を見てピンときた人は鋭いです。
$$\frac12 mv_2^2 – \frac12 mv_1^2 = mgh\tag{1:再掲}$$
等加速度運動公式
$$v_2^2-v_1^2=2as$$
に近い形をしています。
両辺に $2$ を掛けて $m$ で割り、
さらに $g$ を $a$ と、高さ $h$ を $s$ と書くとそうなります。
つまり、物体の落下は、
エネルギー保存の法則で解いても
等加速度運動で解いても
全く同じです。
関連:等加速度運動の3公式を微積で導く
重力の位置エネルギー:仕事が蓄えられると捉える
ここからは、位置エネルギーを「仕事が蓄えられる」という視点で見直してみます。 この考え方は、符号の理解にもつながる大切なポイントです。
重力の位置エネルギーは「重力が行った仕事」で定義できますが、
逆向きの視点
で考えると、より直感的に理解できます。
あなたが物体を持ち上げる:あなたの仕事が蓄えられる
質量 $m$ の物体を高さ $h$ まで持ち上げるとき、
あなたは重力に逆らって仕事をします。
$$W = \int_0^h mg\,dx = mgh$$

このとき、
- あなたがした仕事 $mgh$ が、
- 物体が位置として “蓄えたエネルギー”
です。
つまり、
あなたがした仕事が、そのまま位置エネルギーとして蓄えられた
という見方ができます。
この視点は、
位置エネルギーの符号や意味がしっくりくる
という読者も多く(私もそのうちの一人です)、
重力以外の位置エネルギー(ばね・万有引力)にも自然につながります。
私はこちらの考え方の方が符号の扱いも含めてしっくりくるので、以降はこの視点で統一して進めます。
弾性エネルギー(ばね)
ばねの力は
$$F_{ばね}=-kx$$
あなたがばねに与える力は
$$F_{あなたの手}=kx$$

あなたの手がばねを $0$ から $x$ までゆっくり伸ばすと、
$$W=\int_0^x kx\,dx = \frac12 kx^2$$
これが 弾性エネルギー です。
弾性エネルギー: $\displaystyle\frac{1}{2}kx^2$
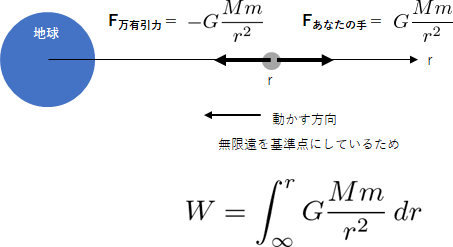
万有引力の位置エネルギー
物体に働く万有引力は
$$F_{万有引力}=-G\frac{Mm}{r^2}$$
あなたが万有引力に逆らって物体に与える力は
$$F_{あなたの手}=G\frac{Mm}{r^2}$$

あなたの手が物体を $\infty$ から $r$ まで運ぶと、
\begin{eqnarray}
W &=& \int_\infty^r G\frac{Mm}{r^2}\,dr\\
&=& -G\frac{Mm}{r}
\end{eqnarray}
位置エネルギーが負になるのは、
加えている力と逆の方向に運んでいるからです(負の仕事をしているから)。
万有引力の位置エネルギー: $-\displaystyle G\frac{Mm}{r}$
電位(電荷の位置エネルギー)
電荷 $+Q$ が電荷 $+q$ に及ぼす力(静電気力)は
$$F_{静電気力}=k\frac{Qq}{r^2}$$
あなたが静電気力に逆らって電荷に与える力は
$$F_{あなたの手}=-k\frac{Qq}{r^2}$$

あなたの手が電荷を $\infty$ から $r$ まで運ぶと、
\begin{eqnarray}
W &=& \int_\infty^r \left(-k\frac{Qq}{r^2}\right)\,dr\\
&=& k\frac{Qq}{r}
\end{eqnarray}
ただし、電位 $V$ は「 $q=+1\mathrm{[C]}$ あたりの位置エネルギー」なので、
$V=\displaystyle k\frac{Q}{r}$
関連:電位のグラフが共通テストで出題
まとめ:エネルギー保存の本質
まずはこれまで求めてきた位置エネルギーを表にまとめます。
| 力の種類 | 力の式 | 位置エネルギー | 備考 |
|---|---|---|---|
| 重力 | $F=-mg$ | $mgh$ | 基準高さを $h=0$ とする |
| ばね(弾性力) | $F=-kx$ | $\displaystyle \frac12 kx^2$ | 自然長を $x=0$ とする |
| 万有引力 | $\displaystyle -G\frac{Mm}{r^2}$ | $\displaystyle -G\frac{Mm}{r}$ | $r=\infty$ を基準にする |
| 静電気力(電位) | $\displaystyle k\frac{Qq}{r^2}$ | $\displaystyle k\frac{Qq}{r}$ | $q=1\mathrm{[C]}$ あたりが電位 $V$ |
運動方程式は
瞬間瞬間の力と運動
を表す式。それを積分すると
最初と最後だけで物事を捉える式
になります。これが 力学的エネルギー保存の法則
そして、
運動方程式もエネルギー保存の法則も本質的には同じ内容です。
どちらを使うかは「どちらが楽か」というだけで、
エネルギーの視点を使うと、
途中経過を追わずに最初と最後だけで議論できる
という大きな利点があります。
関連:運動量保存の法則も運動方程式の積分で導ける


コメント