2つの波源から出る波の干渉を3Dアニメーションで確認します。それにより、強めあう条件や弱めあう条件の意味が理解でき、この後のヤングの実験の基礎ができます。
ヤングン実験の記事はこちら↓です。
問題設定：$\lambda=2\pi$, $\mathrm{AB}=6\pi$, 同位相
問題：腹の本数と節の本数
腹になる本数、節になる本数はそれぞれ何本？
強めあう条件（腹の条件）と弱めあう条件（節の条件）はそれぞれ、
腹の条件：$\overline{\mathrm{PA}}-\overline{\mathrm{PB}}=m\lambda$
節の条件：$\overline{\mathrm{PA}}-\overline{\mathrm{PB}}=\left(m+\displaystyle\frac{1}{2}\right)\lambda$
です。これは差が一定の軌跡なので双曲線です。
解：腹7本、節5本
腹の数
腹の条件は、
$\overline{\mathrm{PA}}-\overline{\mathrm{PB}}=m\lambda\quad$ ($m$ は整数)
$\overline{\mathrm{AB}}=6\pi$, $\lambda=2\pi$ より、
$$-6\pi\le\overline{\mathrm{PA}}-\overline{\mathrm{PB}}=m\cdot 2\pi\le6\pi$$
よって、
$$m=\pm3,\,\pm 2,\,\pm 1,\,0$$
の7本。
節の数
節の条件は、
$\overline{\mathrm{PA}}-\overline{\mathrm{PB}}=\left(m+\displaystyle\frac{1}{2}\right)\lambda\quad$ ($m$ は整数)
$\overline{\mathrm{AB}}=6\pi$, $\lambda=2\pi$ より、
$$-6\pi\le\overline{\mathrm{PA}}-\overline{\mathrm{PB}}=\left(m+\displaystyle\frac{1}{2}\right)\cdot 2\pi\le6\pi$$
よって、
$$m=-3,\,-2,\,-1,\,0,\,1,\,2$$
の5本。
解説：$\overline{\mathrm{PA}}-\overline{\mathrm{PB}}$ を $-6\pi$ と $ 6\pi$ ではさむとは
ここでは、$\overline{\mathrm{PA}}-\overline{\mathrm{PB}}$ を $-6\pi$ と $6\pi$ ではさむことについて理解します。つまり、
$$-6\pi\le\overline{\mathrm{PA}}-\overline{\mathrm{PB}}\le6\pi$$
についてですが、$\overline{\mathrm{PA}}-\overline{\mathrm{PB}}$ が最も小さくなるのは $\mathrm{P}$ が $\mathrm{A}$ と重なるとき（と補足のとき）で↓の絵のときです。
このとき、
\begin{eqnarray}
\overline{\mathrm{PA}} &=& 0\\
\overline{\mathrm{PB}} &=& 6\pi
\end{eqnarray}
なので、
$$\overline{\mathrm{PA}}-\overline{\mathrm{PB}}=-6\pi$$
です。逆に最大になるのは $\mathrm{P}$ が $\mathrm{B}$ と重なるときで、このときは
\begin{eqnarray}
\overline{\mathrm{PA}} &=& 6\pi\\
\overline{\mathrm{PB}} &=& 0
\end{eqnarray}
なので、
$$\overline{\mathrm{PA}}-\overline{\mathrm{PB}}=6\pi$$
です。
補足
ここは
$\overline{\mathrm{PA}}-\overline{\mathrm{PB}}$ が最も小さくなるのは $\mathrm{P}$ が $\mathrm{A}$ と重なるとき
の補足です。
$\overline{\mathrm{PA}}-\overline{\mathrm{PB}}$ が最小の $-6\pi$ になるのは $\mathrm{P}$ が $\mathrm{A}$ と重なるとき以外に
$\mathrm{P}$ が直線 $\mathrm{AB}$ 上で $\mathrm{A}$ に対して $\mathrm{B}$ と反対側
も同様に $-6\pi$ です。↓の絵の紫の線です。
例えば↑の絵の点 $\mathrm{P}$ は $(-5\pi,0)$ ですが、このとき、
\begin{eqnarray}
\overline{\mathrm{PA}} &=& 2\pi\\
\overline{\mathrm{PB}} &=& 8\pi
\end{eqnarray}
なので、
$\overline{\mathrm{PA}}-\overline{\mathrm{PB}}=-6\pi$
です。
3次元アニメーションでイメージを膨らませる
アニメーション
1章で説明した内容を実際の3Dアニメーションで確認します。
静止画で確認
個別の波を描画するとこのようになります。
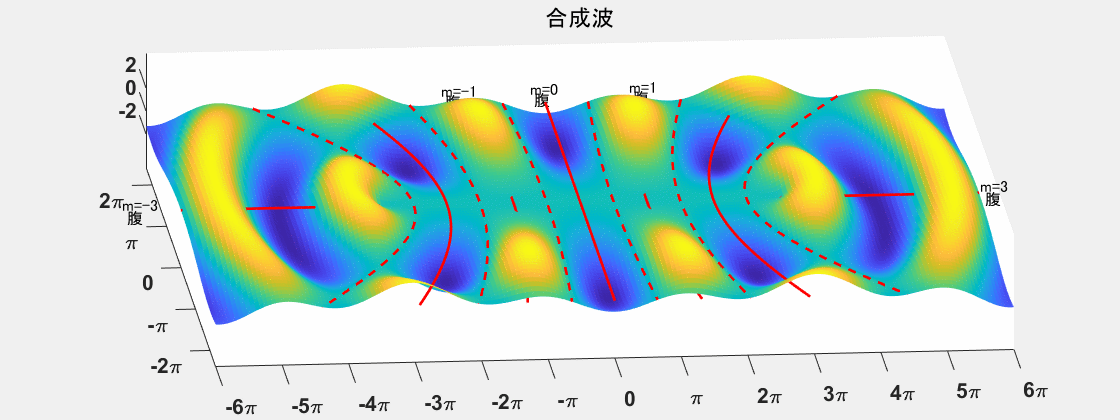
しかし実際には個別に波を観測することはできません。合成波になります。↓のようになります。
これを上から見ると↓のようになります。
ここに腹と節を重畳させます。腹は実線、節は点線で書いています。腹は実線ですが、波の下側に入ってしまっている部分は消えていることに注意してください。なお、実線、点線ともに双曲線です。
ここから先は前出の絵の復習です。腹と節を重畳した状態で今一度視点を斜めにします。
最初の絵に戻すべく、個別の波です。
まとめ
2つの波源から出る波の干渉をアニメーションで確認しました。干渉した結果、腹と節がそれぞれ双曲線状にできるイメージがついたと思います。このイメージを持って、強めあう条件の式、弱めあう条件の式を立てるようにしましょう。
コメント