合成関数 $(y=f(g(x)))$ の微分は、「外側 $(y=f(X))$」と「内側 $(X=g(x))$」の変化が同時に起きるため、最初はつかみにくく感じます。しかし、図形とアニメーションでイメージをつかむと、かっこのままで微分できる理由が自然に理解できます。
さらに 連鎖律 (chain rule) という概念が理解できれば、合成関数の微分がいとも当たり前に感じられることでしょう。
これらが理解できれば、置換積分(かっこのまま積分)にも自然につながります。
また、合成関数の微分と並んでつかみにくい「積の微分」も、展開のアニメーションで理解できます。この記事のあとに読むと理解が深まります。
合成関数の微分は「変化の二段階伝達」
合成関数とは、
$$y = f(g(x))$$
のように、x → X=g(x) → f(X) と変化が二段階で伝わる関数です。つまり、
$x$ が動くと、$X=g(x)$ が動き、さらに $f(X)$ が動く
という「変化の伝言ゲーム」になっています。これが連鎖律の本質です。
イメージで理解:変化が二段階で伝わる様子
例として、
$$y = (2x – 1)^2$$
を考えます。ここでは、$X = 2x – 1$ と置くことで、
$$y = X^2$$
と見なしてアニメーションで変化を追います。
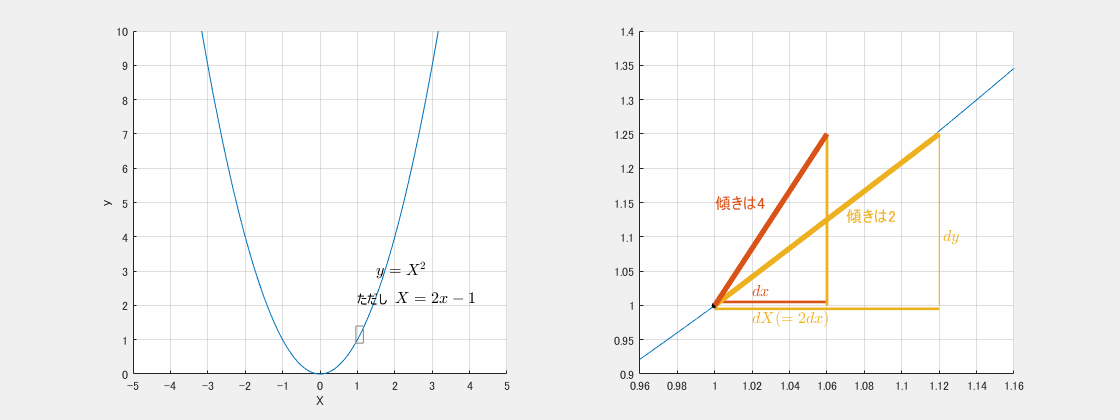
左図は $y=X^2$ のグラフ、右図はその拡大図です。黄が $X$ の変化を表しています。まずは $y$ を $X$ で微分するので、これは左図の青のグラフの接線の傾きになります。
まずは $X$ で微分する:黄の傾き(=青の傾き)
$y=X^2$ の微分は、
$$\frac{dy}{dX} = 2X\tag{1}$$
これはアニメーションの黄の傾きに対応します。すなわち、青の傾きを求めていることになります。
$x$ と $X$ の歩みの違い:赤はゆっくり進む
$X = 2x – 1$ の微分は、$\displaystyle\frac{dX}{dx} = 2$ なので、$x$ が $dx$ 進むと、
$$dX=2\,dx\tag{2}$$
つまり、黄は赤の2倍速く進むということです。
主役は $x$ の変化
ここで視点を「$x$ の変化」に戻しましょう。求めたかったのは、$x$ が微小に変化したときに $y$ がどれだけ変化するか、ということでした。上記を組み合わせると、
$x$ が $dx$ 進むと、$X$ は $2\,dx$ 進む。(2)
$X$ が $dX$ 進むと、$y$ は $2X$$\,dX$ 進む。(1)
つまり、$x$ が $dx$ 進むと、$y$ は $2X$$\cdot$$2\,dx$ 進む。
ということになっています。ここで「外側の変化(1) × 内側の変化(2)」という連鎖律の構造が、図形的にもはっきり見えてきます。
このように、$X$ を介して $x$ の変化が $y$ の変化に及ぶという、二段階で伝わっていくことが分かります。
微分の連鎖律 (chain rule)
ここまでの流れを式にすると、実は上記は、
$$\frac{dy}{dx} = \frac{dy}{dX} \cdot \frac{dX}{dx}\tag{3}$$
と形式的に書くことができます。つまり、
- (1): $y=X^2$ より、$\displaystyle\frac{dy}{dX}=2X$
- (2): $X=2x-1$ より、$\displaystyle\frac{dX}{dx}=2$
- (3): $\displaystyle\frac{dy}{dx} = \displaystyle\frac{dy}{dX} \cdot \displaystyle\frac{dX}{dx}=2X\cdot 2$
\begin{eqnarray}
\frac{dy}{dx} &=& 2X\cdot2\\
&=& 2(2x-1)\cdot 2
\end{eqnarray}
連鎖律の本質:分数の鎖がつながる
式変形を振り返ると、
$$\frac{dy}{dx}=\frac{dy}{\cancel{dX}}\cdot\frac{\cancel{dX}}{dx}$$
となっており、普通の分数のように “つながる” イメージが連鎖律(chain rule)の本質です。
例題で確認する
例1:$y=(2x-1)^2$ をかっこのままで微分
\begin{eqnarray}
\displaystyle\frac{dy}{dx} &=& \displaystyle\frac{d(2x-1)^2}{d(2x-1)}\cdot\displaystyle\frac{d(2x-1)}{dx}\\
&=& 2(2x-1)\cdot 2
\end{eqnarray}
例2:$y=\sin^2 x$ の微分
$X=\sin x$ と置くと $y=X^2$ なので、
- $\displaystyle\frac{dy}{dX} = 2X$
- $\displaystyle\frac{dX}{dx} = \cos x$
よって、
\begin{eqnarray}
\displaystyle\frac{dy}{dx} &=& \displaystyle\frac{d\sin^2 x}{d\,\sin x}\cdot\displaystyle\frac{d\,\sin x}{dx}\\
&=& 2\sin x\cdot\cos x
\end{eqnarray}
これも「かっこのまま微分」の型で理解できます。
まとめ
合成関数の微分(連鎖律)は、変化が二段階で伝わるというイメージで理解できます。分数の鎖がつながるように、
$$\frac{dy}{dx}=\frac{dy}{\cancel{dX}}\cdot\frac{\cancel{dX}}{dx}$$
と考えると、かっこのままで微分できる理由が自然に見えてきます。
この考え方は置換積分にも直結します。詳しくは次の記事で解説しています。
なお、「積の微分」も合成関数と同じくイメージがつかみにくいテーマですが、これもアニメーションで理解できます。こちらの記事もあわせてどうぞ。

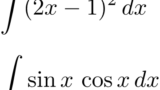


コメント