直線に関して対称な点は、内積(射影ベクトル)の考え方が分かれば一発で求められます。
ただ、いきなり射影ベクトルは難しいと感じる人も多いので、この記事では「初級 → 中級 → 上級」と段階を踏みながら、5つの方法を紹介します。
計算量は多いけれど理屈が分かりやすい方法から、
最速で求められる裏ワザ級の方法まで揃えていますので、
自分に合った解き方を見つけてみてください。
直線 $y=2x+1$ に関して、点 $\mathrm{P}(-1,4)$ と対称な点を $\mathrm{Q}$ とするとき、点 $\mathrm{Q}$ の座標を求めよ。
1. 初級:連立方程式で解く方法
考え方($\mathrm{Q}$ が満たすべき連立方程式で $\mathrm{H}$ を求める)
この解法は理屈は簡単ですが、その分計算量が多く面倒です。
求めたい点 $\mathrm{Q}$ を $(a,b)$ と置いて連立方程式を立てます。
現時点では点 $\mathrm{Q}$ がどこにあるのかわからない状態なので、点 $\mathrm{Q}$ が彷徨うイメージです。
点 $\mathrm{Q}$ がどこか分からないので彷徨っています。
しかし、点 $\mathrm{H}$ は点 $\mathrm{Q}$ に応じて定まる点です。
青の線と赤の線が垂直で、かつ点 $\mathrm{H}$ が青の直線上にあるようなところを探しています。
計算例
点 $\mathrm{Q}$ の座標を $(a,b)$ と置く。
このとき、$\mathrm{PQ}$ の傾きは
$$\frac{b-4}{a-(-1)}$$
であり、それが傾き $-\displaystyle\frac12$ になればよいから、
$$\frac{b-4}{a-(-1)}=-\frac12\tag{1}\label{p1355eq1-1}$$
一方、このとき点 $\mathrm{H}$ の座標は
$$\left(\frac{-1+a}{2},\,\frac{4+b}{2}\right)$$
であり、この点が直線 $y=2x+1$ 上にあるから、
$$\frac{4+b}{2}=2\times\frac{-1+a}{2}+1\tag{2}\label{p1355eq1-2}$$
\eqref{p1355eq1-1}, \eqref{p1355eq1-2} を解いて、
$$a=3,\; b=2$$
よって、
$$\mathrm{Q}(3,2)$$
2. 初級:垂線との交点で解く方法
考え方(垂線との交点で $\mathrm{H}$ を求める)
点 $\mathrm{P}$ を通り直線 $y=2x+1$ に垂直な直線との交点 $\mathrm{H}$ を求め、
同じだけ向こう側が求める点 $\mathrm{Q}$ です。
点 $\mathrm{P}$ を通り傾き $-\displaystyle\frac12$ の赤の線が表れることで、
その線と青の線との交点 $\mathrm{H}$ が求まります。
その後、 $\mathrm{P}$ から $\mathrm{H}$ までの道のりを数え、
同じだけ $\mathrm{H}$ から進んだところが求めるべき点 $\mathrm{Q}$ です。
計算例
点 $\mathrm{P}(-1,4)$ を通り傾き $-\displaystyle\frac{1}{2}$ の直線の方程式は、
$$y=-\frac{1}{2}(x+1)+4\tag{1}\label{p1355eq2-1}$$
元の直線
$$y=2x+1\tag{2}\label{p1355eq2-2}$$
との交点を $\mathrm{H}$ とすると、 \eqref{p1355eq2-1}, \eqref{p1355eq2-2} を解いて、
$$\mathrm{H}(1,3)$$
求める点 $\mathrm{Q}$ は、さらに $\mathrm{PH}$ と同じだけ進んだ点なので、
$$\mathrm{Q}(3,2)$$
補足:直線の式を一行で書く裏ワザ
関連:直線の式を超速で求める方法
\eqref{p1355eq2-1}のように一行で書けるようになりたいです。
3. 中級:ベクトル方程式で解く方法
考え方($\mathrm{H}$ までの媒介変数値を倍にすると $\mathrm{Q}$)
ベクトル方程式を使えば垂線の方程式が簡単に立てられます。
その交点 $\mathrm{H}$ を示す媒介変数の倍の値が対称点 $\mathrm{Q}$ を与えます。
初級では「連立方程式」や「直線の式」を毎回作る必要がありますが、
法線ベクトルを使うと 直線の向きそのものを利用できるため、計算が一気にシンプル になるのです。
法線ベクトルの概念はこちら↓
ベクトル方程式は、ベクトルの長さを調整する変数(媒介変数)を使って行き先を規定するものです。
計算例
直線 $2x−y=−1$ の法線ベクトルは $\begin{pmatrix}2 \\ -1\end{pmatrix}$。
点 $\mathrm{P}(-1,4)$ を通りこの法線ベクトルを持つ直線は媒介変数 $t$ を使って、
$$\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}-1 \\ 4\end{pmatrix}+t\begin{pmatrix}2 \\ -1\end{pmatrix}$$
これが直線 $2x-y=-1$ と交わる点 $\mathrm{H}$ は、
$$2(-1+2t)-(4-t)=-1$$
より、
$$t=1$$
さらに同じだけ進むと点 $\mathrm{Q}$ で、
$$t=2$$
よって、
$$\mathrm{Q}(3,2)$$
4. 上級:直線方向に射影する方法
考え方(射影ベクトルで $\mathrm{H}$ を求める)
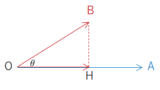
$\overrightarrow{\mathrm{QP}}$ を $\overrightarrow{\mathrm{QA}}$ 上に射影して点 $\mathrm{H}$ を求めます。
点 $\mathrm{H}$ が求まれば、 そこからさらに $\overrightarrow{\mathrm{PH}}$ だけ進んで点 $\mathrm{R}$ を求めます。
なお、$\overrightarrow{\mathrm{QA}}$ はより単純な $\begin{pmatrix}1 \\ 2 \end{pmatrix}$ でもかまいませんが、
求めるべき $\overrightarrow{\mathrm{QH}}$ との混同を避けるため、あえて $\begin{pmatrix}2 \\ 4 \end{pmatrix}$ にしています。
(自分でやるときは $\begin{pmatrix}1 \\ 2 \end{pmatrix}$ でかまいません。)
※ここでは、直線上の基準点を $\mathrm{Q}$、対称な点を $\mathrm{R}$ としています。
射影ベクトルを使えば、垂線の足が一発で求まります。
計算例
$\mathrm{Q}(0,1)$、$\mathrm{A}(2,5)$ とすると、$\mathrm{P}(-1,4)$ とから
$$\begin{eqnarray}
\overrightarrow{\mathrm{QH}} &=& \frac{\overrightarrow{\mathrm{QA}}\cdot\overrightarrow{\mathrm{QP}}}{|\overrightarrow{\mathrm{QA}}|^2}\cdot\overrightarrow{\mathrm{QA}}=\frac{\begin{pmatrix}2 \\ 4 \end{pmatrix}\cdot\begin{pmatrix}-1 \\ 3 \end{pmatrix}}{\left|\begin{pmatrix}2 \\ 4 \end{pmatrix}\right|^2}\cdot\begin{pmatrix}2 \\ 4 \end{pmatrix}\\
&=& \begin{pmatrix}1 \\ 2 \end{pmatrix}
\end{eqnarray}$$
よって $\mathrm{H}(1,3)$。ここからさらに $\overrightarrow{\mathrm{PH}}=\begin{pmatrix}2 \\ -1\end{pmatrix}$ だけ進むと、
$$\mathrm{R}(3,2)$$

5. 上級:法線方向に射影する方法(本命)
考え方(射影ベクトルで $\overrightarrow{\mathrm{PH}}$ を直接求める)
法線方向がすでに分かっているので、この方向に直接射影すれば一発で $\overrightarrow{\mathrm{PH}}$ が求まります。そこから同じだけ進めば対称点 $\mathrm{R}$ です。
※ここでは、直線上の基準点を $\mathrm{Q}$、対称な点を $\mathrm{R}$ としています。
法線ベクトルを使う射影は、
「点と直線の距離」「点と平面の距離」でも使えるため非常に便利です。
計算例
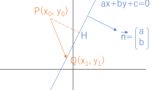
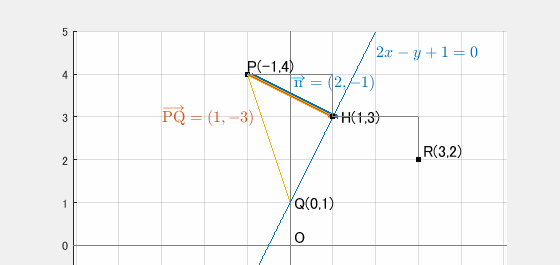
直線 $2x-y+1=0$ の法線ベクトルは $\overrightarrow{n}=\begin{pmatrix}2\\-1\end{pmatrix}$
点 $\mathrm{P}(-1,4)$ から直線に下した垂線の足 $\mathrm{H}$ は、
直線 $y=2x+1$ 上の点の一つ $(0,1)$ を $\mathrm{Q}$ と置いて、
$$\begin{eqnarray}
\overrightarrow{\mathrm{PH}} &=& \frac{\overrightarrow{\mathrm{PQ}}\cdot\overrightarrow{n}}{|\overrightarrow{n}|^2}\cdot\overrightarrow{n} = \frac{\begin{pmatrix}1 \\ -3 \end{pmatrix}\cdot\begin{pmatrix}2 \\ -1 \end{pmatrix}}{\left|\begin{pmatrix}2 \\ -1 \end{pmatrix}\right|^2}\cdot\begin{pmatrix}2 \\ -1 \end{pmatrix}\\
&=& \begin{pmatrix}2 \\ -1 \end{pmatrix}
\end{eqnarray}$$
よって $\mathrm{H}(1,3)$。ここからさらに $\overrightarrow{\mathrm{PH}} = \begin{pmatrix}2 \\ -1 \end{pmatrix}$ だけ進むと、
$$\mathrm{R}(3,2)$$

まとめ:状況別の最適な解法と使い分け
直線に関して対称な点を複数の解法で解きました。
最後に、状況に応じた使い分けをまとめます。
状況別のおすすめ解法
| 状況 | おすすめの方法 | 理由 |
|---|---|---|
| 基本を理解したい | 初級(連立方程式・垂線) | 理屈が簡単 |
| 計算量を減らしたい | 中級(ベクトル方程式) | 理屈が比較的簡単で手順が短い |
| 最速で求めたい | 上級(射影ベクトル) | ほぼ一発で求まる |
また、射影ベクトルの考え方は「点と直線の距離」でもそのまま使えます。



コメント