この記事では下記の動画を例題として挙げ、「パラメータを消すとなぜ軌跡が求まるのか」を本質から理解します。
教科書や解答では「$m$ を消去して軌跡を求める」とさらっと書かれますが、
- なぜパラメータ $m$ を代入すると軌跡が出るのか?
- なぜ $x=0$ で場合分けしないといけないのか?
- 「分母が0になるから」という説明だけではモヤモヤする
と感じる人も多いと思います。
この記事では、まず動画でイメージをつかみ、次に最短ルートの解法を確認し、そのうえで「なぜそうなるのか」という本質を丁寧に言葉にしていきます。最後に、少しだけ設定を変えた類題(問題2)で理解を定着させます。
問題1:$mx-y=0$, $x+my=1$
まずは、今回のメインとなる問題です。
2直線 $mx-y=0$, $x+my=1$ がある。$m$ が実数全体を動くとき、2直線の交点 $\mathrm{P}(x,y)$ の軌跡を求めよ。
この投稿ではじっくりと本質から説明しますが、まずはサクッと解法だけ知りたいという場合は、次の記事も参考になります。
該当箇所に直接行きたい場合はこちら。
まずはイメージをつかむ(動画)
2直線にはパラメータ $m$ が入っています。これは、
$m$ が決まる $\Rightarrow$ 2直線が決まる $\Rightarrow$ 交点 $\mathrm{P}$ が決まる
という関係です。$m$ を動かすと交点 $\mathrm{P}$ も動き、その動きが「交点の軌跡」になります。
動画を見ると、交点はどうやら
- 中心 $\left(\dfrac12,0\right)$
- 半径 $\dfrac12$ の円
- ただし原点 $(0,0)$ は通らない
という軌跡を描いているように見えます。
このイメージを持ったまま、次に最短ルートの解法を確認します。
最短ルートで軌跡を求める(解)
まずは教科書的な解法です。ここでは「なぜそうするのか」よりも、「どう解くか」を先に確認します。
解
$$mx-y=0\tag{1}$$ $$x+my=1\tag{2}$$
(i) $x\ne 0$ のとき
(1) より $m=\dfrac{y}{x}$。これを (2) に代入すると、
$$x+\frac{y}{x}y=1$$ 両辺に $x$ をかけて $$x^2+y^2=x$$
整理すると、
$$\left(x-\frac12\right)^2+y^2=\frac14\tag{3}$$
ただし $x\ne 0$ より $(0,0)$ は除く。
(ii) $x=0$ のとき
(1) より $y=0$。しかし $(0,0)$ を (2) に代入すると
$$0+m\cdot 0=1$$
となり、どんな $m$ でも成り立たない。したがって $(0,0)$ は条件を満たさない。
(i)(ii) より
中心 $\left(\dfrac12,0\right)$、半径 $\dfrac12$ の円。ただし $(0,0)$ を除く。
モヤモヤポイント
ここまでで「どう解くか」は確認できました。ただ、皆さんが本当に知りたいのは「なぜそうするのか」です。モヤモヤを言語化すると、次の2点に集約されます。
- なぜ $m=\dfrac{y}{x}$ を代入すると「交点の軌跡」になるの?
- なぜ $x\ne 0$ と $x=0$ で場合分けするの?
ここからは、このモヤモヤを一つずつ解消していきます。
なぜ m を消すだけで軌跡が出るのか(本質)
ひとことで言えば、
$m$ を消すとは、(1)(2) を同時に満たす点 $(x,y)$ を求めること
だからです。つまり交点を求めているということです。
ただし、ここがモヤモヤしているという前提で、もう少し丁寧に見ていきます。
$m=\dfrac{y}{x}$ の意味
$m=\dfrac{y}{x}$ は、点 $(x,y)$ を通るように (1) の直線 $mx-y=0$ の傾きを逆算した式です。例えば、
- $(1,2)$ → $m=2$
- $(1,1)$ → $m=1$
- $\left(\dfrac12,\dfrac12\right)$ → $m=1$
つまり、
点 $(x,y)$ を通るように (1) の傾き $m$ を決める式
になっています。
「これを (2) に代入する」とは何をしているのか
点 $(x,y)$ を通るように決めた $m$ を (2) に代入し、
(2) も満たす点だけを残す(プロットする)
という操作をしています。
例えば、$(1,1)$ は (1) を満たすので $m=1$ ですが、(2) $x+my=1$ に代入すると成り立たないため除外されます。

一方、$\left(\dfrac12,\dfrac12\right)$ は (1) から $m=1$ となり、(2) に代入しても成り立つため残ります。

つまり、
(1) も (2) も満たす点=交点をふるいにかけている
ということです。
(1) を (2) に代入した式を眺める
(1) を (2) に代入すると、
$$x+\frac{y}{x}y=1\tag{4}$$
となります。これは、(1)(2) を同時に満たす点だけが成り立つ式なので、
交点の軌跡を表す式
になっているわけです。
なぜ $x\ne 0$ と $x=0$ で場合分けするのか
形式的には「$m=\dfrac{y}{x}$ の分母が 0 になるから」ですが、もう少し本質的に見ると、
$x=0$ では点 $(x,y)$ に対応する $m$ が決まらないケースがある
ということです。例えば $(0,1)$ では、(1) を満たす $m$ は存在しません。つまり、
- $x\ne 0$:対応する $m$ が必ず決まる
- $x=0$:対応する $m$ が決まらない点がある
この性質の違いがあるため、$x=0$ のときだけは別建てで調べる必要があります。
問題2:$mx-y=0$, $x+my=m$
ここまでの理解をさらに定着させるために、少しだけ設定を変えた類題を扱います。基本的な流れは問題1と同じですが、例外処理の結果が少し変わります。
2直線 $mx-y=0$, $x+my=m$ がある。$m$ が実数全体を動くとき、2直線の交点 $\mathrm{P}(x,y)$ の軌跡を求めよ。
問題1の2直線は $mx-y=0$, $x+my=1$ でした。右辺が $1$ から $m$ に変わっただけですが、挙動が少し変わります。
まずはイメージをつかむ(動画)
先ほどと同様に、まずは $m$ を動かしたときの交点の動きを動画で眺めます。
動画を見ると、交点は次のように動きます。
- 原点 $(0,0)$ は通る
- $(0,1)$ は通らない
- 交点の軌跡は、中心 $\left(0,\dfrac12\right)$、半径 $\dfrac12$ の円
問題1と似ていますが、原点を通る点が追加されているのが特徴です。
最短ルートの解法
問題1と同じ流れで、まずは最短ルートの解法を確認します。
解
$$mx-y=0\tag{1}$$ $$x+my=m\tag{2}$$
(i) $x\ne 0$ のとき
(1) より $m=\dfrac{y}{x}$。これを (2) に代入すると、
$$x+\frac{y}{x}y=\frac{y}{x}$$ 両辺に $x$ をかけて $$x^2+y^2=y$$
整理すると、
$$x^2+\left(y-\frac12\right)^2=\frac14\tag{3}$$
ただし $x\ne 0$ より、$(0,0)$, $(0,1)$ は除く。
(ii) $x=0$ のとき
(1) より $y=0$。これを (2) に代入すると、
$$0+m\cdot 0=m$$
となり、$m=0$ のとき成り立つ。したがって $(0,0)$ は条件を満たす。
(i)(ii) より
中心 $\left(0,\dfrac12\right)$、半径 $\dfrac12$ の円。ただし $(0,1)$ を除く。
例外処理の意味をもう一度かみしめる
例外処理は (ii) の「$x=0$ のとき」です。(3) の円と $x=0$ の直線 の交点を図示すると、赤〇が現れます。

この赤〇が軌跡に含まれるかどうかは、
- 含まれる:その点を (1)(2) 同時に満たす $m$ が存在する
- 含まれない:同時に満たす $m$ が存在しない
という基準で判断します。実際に調べると、
- $(0,0)$ は (1)(2) を同時に満たす $m=0$ がある → 軌跡に含まれる
- $(0,1)$ は (1) を満たさない → 軌跡に含まれない
動画でも $(0,1)$ は $m=\infty$ の極限でしか近づかない点として現れていました。
ここで大事なのは、
パラメータ $m$ が決められない点だけ、
別建てで直接チェックする
という姿勢です。
まとめ
パラメータを含む2式からパラメータを消去するとは、言い換えれば
「2本の式を同時に満たす点 $(x,y)$ を求める」=「連立方程式を解く」
ということです。
連立方程式の解はグラフの交点です。$m$ を動かすと交点が動き、その集合が「交点の軌跡」になります。したがって、
パラメータを消去して得られた式は、
そのまま「交点の軌跡」を表す式になっている
というわけです。
また、$m=\dfrac{y}{x}$ のように分母に変数が来る形では、「分母が0になる」ことがあります。その部分だけは、
いったん除外しておき、
後から別建てで「本当に交点になり得るか」を直接確かめる
というのが、今回の2つの問題で共通していた流れでした。
動画と図でイメージをつかみ、式で本質を確認することで、「パラメータを消す」という一見形式的な操作の裏にある意味が、あなたの中で少しでもクリアになっていたら嬉しいです。

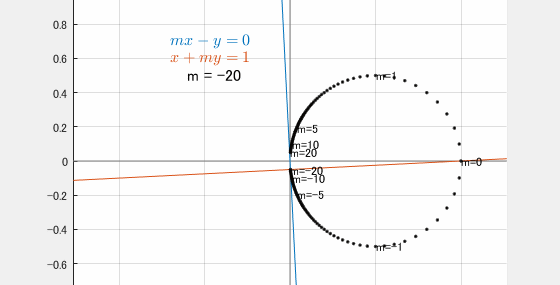

コメント
めっちゃすっきりしました
ありがとうございます 😭
コメントありがとうございます。励みになります!