過去問は「解いて終わり」ではなく、繰り返し解いて実力をつける教材です。本番の共通テストでは丁寧な誘導がありますが、ここではあえて誘導を省き、自分で見通しを立てる練習ができるようにしています。誘導なしで考えることで、理解が一段深まり、復習としての価値が高まります。
IA:第1問 平方根の小数部分
$\sqrt{13}$ を小数2桁目まで求めたい。次の要領で求めよ。
$2\sqrt{13}$ の小数部分を $a$ と置き、$\displaystyle\frac{1}{a}$ を有理化する。
問題をシンプルにしているため取り掛かりづらいかもしれません。実際の共通テストでは丁寧な誘導がついており、自然と導かれるようになっています。しかしここではあえて誘導を省き、「自分で見通しを立てる」練習として扱います。
解. 平方根の小数部分を範囲評価で求める
整数部分を不等式で求める
$2\sqrt{13}$ の小数部分が $a$ なので、まず整数部分を求めます。$2\sqrt{13}=\sqrt{52}$ に注意して、
$$\sqrt{49} < \sqrt{52} < \sqrt{64}$$
より、
$$7 < 2\sqrt{13} < 8$$
したがって整数部分は $7$。
有理化して範囲を絞り込む
整数部分は $7$ と分かったので、
$$a = 2\sqrt{13} – 7$$
となります。ここから $\displaystyle\frac{1}{a}$ を有理化すると、
\[ \frac{1}{a} = \frac{1}{2\sqrt{13}-7} = \frac{2\sqrt{13}+7}{52-49} = \frac{2\sqrt{13}+7}{3} \]
$7<2\sqrt{13}<8$ を使って範囲を絞ると、
\[ \frac{14}{3} < \frac{1}{a} < \frac{15}{3} \]
よって、
\[ \frac{3}{15} < a < \frac{3}{14} \]
$a=2\sqrt{13}-7$ を戻すと、
\[ 7+\frac{3}{15} < 2\sqrt{13} < 7+\frac{3}{14} \]
\[ 3.6 < \sqrt{13} < 3.607\cdots \]
したがって、小数2桁目までは、
$$3.60$$
となります。
IA:第5問 メネラウスの定理・方べきの定理
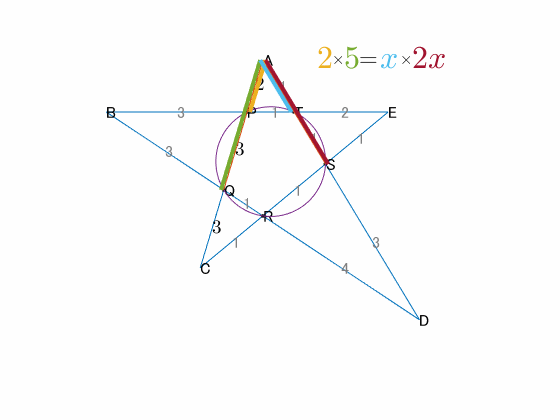
図の星形は次の条件を満たす。
- $\mathrm{AP}=2$, $\mathrm{PQ}=3$, $\mathrm{QC}=3$
- $\mathrm{AT}:\mathrm{TS}:\mathrm{SD}=1:1:3$
- 5点 $\mathrm{P}$, $\mathrm{Q}$, $\mathrm{R}$, $\mathrm{S}$, $\mathrm{T}$ は同一円周上にある。
このとき、
(1) 他の辺の長さを求めよ。
(2) 3点 $\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$ を通る円に対し、点$\mathrm{D}$ はこの円の内側・周上・外側いずれにあるか?

$\mathrm{AP}$, $\mathrm{PQ}$, $\mathrm{QC}$ は長さが分かっています。一方、$\mathrm{AT}$, $\mathrm{TS}$, $\mathrm{SD}$ は比だけが分かっていて長さは不明です。しかし、$\mathrm{AD}$ が決まれば $\mathrm{S}$, $\mathrm{T}$ が決まります。
さらに「5点が同一円周上」という条件が加わることで、星形は完全に決まります。次のアニメーションがそのイメージです。(最後の緑の円が(2)の対象)
解(1). 各辺の比と長さを求める
(1) メネラウスの定理:各辺の比を求める
(i) QR:RD
メネラウスの定理を適用すると、下記の動画。
よって、$\mathrm{QR}:\mathrm{RD}=1:4$。
(ii) 同様に定理を適用
同様にメネラウスの定理を適用していくと、結果次のようになる。
(2) 方べきの定理:各辺の長さを求める
方べきの定理が主張していることは、
$$\mathrm{AP}\cdot\mathrm{AQ}=\mathrm{AT}\cdot\mathrm{AS}$$
方べきの定理の成り立ちや「なぜそうなるのか」を本質から理解したい場合は、次の記事が参考になります。
(i) $\mathrm{AT},\mathrm{TS},\mathrm{SD}$ を求める
$\mathrm{AT}=x$ と置くと、
\[2\times 5=x\times 2x\\x=\sqrt{5}\]
したがって、
$$\mathrm{AT}=\sqrt{5},\;\mathrm{TS}=\sqrt{5},\;\mathrm{SD}=3\sqrt{5}$$
(ii) 同様に定理を適用
同様に方べきの定理を適用していくと、結果次のようになる。
解(2). 方べきの定理で点Dが円の外側であることを示す
方べきの定理が主張していることは、仮に $\mathrm{D^\prime}$ が円周上とすると、
$$\mathrm{AQ}\cdot\mathrm{QC} = \mathrm{BQ}\cdot\mathrm{QD^\prime}$$
しかし実際には
$$\mathrm{AQ}\cdot\mathrm{QC} < \mathrm{BQ}\cdot\mathrm{QD}$$
なので、点 $\mathrm{D}$ は円の外側にある。
IIB:第1問(2) 整式の割り算
剰余の定理の典型問題です。$P(x)=S(x)T(x)+R(x)$ という式変形がミソ。
$x$ の整式 $P(x)$ を $x$ の2次式 $S(x)$ で割る。
(1) 方程式 $S(x)=0$ が異なる二つの解 $\alpha$, $\beta$ を持つとき、
$P(x)$ を $S(x)$ で割った余りが定数 $\iff$ $P(\alpha)=P(\beta)$
を示せ。
(2) $P(x)=x^{10}-2x^9-px^2-5x$ を $S(x)=x^2-x-2$ で割った余りが定数となるとき、$p$ の値と余りを求めよ。
(1)では「同値」を示すため、$\implies$ と $\impliedby$ の両方を示す必要があります。
左側を出発点にすれば、$P(x)=S(x)T(x)+k$ と置け、
右側を出発点にすれば、$P(x)=S(x)T(x)+mx+n$ と置けます。
(2)では $x^{10}$ や $x^9$ を計算させるのかと身構えますが、実は計算しなくてもよくなるように誘導されています。共通テストらしい“優しさ”が見える問題です。もちろん、(1)の結果を使います。
解(1). 余りが定数 $\iff$ $P(\alpha)=P(\beta)$ を証明する
$S(x)=0$ は異なる解 $\alpha$, $\beta$ を持つことから、
- $\alpha\ne\beta$
- $S(\alpha)=S(\beta)=0$
(i) $\implies$ の証明:余りが定数のとき
$P(x)$ を $S(x)$ で割った商を $T(x)$、余りを $k$ とすると、
$$P(x)=S(x)T(x)+k$$
と書ける。$S(\alpha)=S(\beta)=0$ に注意すると、
\[ \begin{aligned} P(\alpha)&=k\\ P(\beta)&=k \end{aligned} \]
よって、
$$P(\alpha)=P(\beta)$$
(ii) $\impliedby$ の証明:$P(\alpha)=P(\beta)$ のとき
2次式で割るので余りは高々1次式。よって、
$$P(x)=S(x)T(x)+mx+n$$
と書ける。$S(\alpha)=S(\beta)=0$ に注意すると、
\[ \begin{aligned} P(\alpha)&=m\alpha+n\\ P(\beta)&=m\beta+n \end{aligned} \]
$P(\alpha)=P(\beta)$ より、
$$m(\alpha-\beta)=0$$
$\alpha\ne\beta$ なので、
$$m=0$$
したがって余りは定数となる。
解(2). 余りが定数となる $p$ と余りの値を求める
$S(x)=(x-2)(x+1)$ より、$S(x)=0$ の解は $x=2$, $x=-1$。これを
$P(x)=x^{10}-2x^9-px^2-5x$ に代入すると、
\[ \begin{aligned} P(2)&=-4p-10\\ P(-1)&=-p+8 \end{aligned} \]
(1)より、余りが定数となるためには $P(2)=P(-1)$ が必要。
\[ -4p-10=-p+8 \]
\[ \therefore\; p=-6 \]
このときの余りは、
\[ P(2)=14 \]
解説. 実際に割り算をすると
$p=-6$ を $P(x)$ の式に代入すると、
\[\begin{aligned}P(x) &= x^{10}-2x^9+6x^2-5x \\ &=(x-2)(x+1)(x^8-x^7+x^6-x^5+x^4-x^3+x^2-x+7)+14\end{aligned}\]
となり、確かに余りは定数 $14$ になりました。WolframAlphaで確認。
IIB:第2問 微分法・積分法
$m$ は $m>1$ を満たす定数とし、
\[f(x)=3(x-1)(x-m)\\
S(x)=\displaystyle\int_0^xf(t)\, dt\]
とする。そして、
- $S_1$: $0\le x\le 1$ の範囲で、関数 $y=f(x)$ のグラフと $x$ 軸、$y$ 軸で囲まれた図形の面積
- $S_2$: $1\le x\le m$ の範囲で、関数 $y=f(x)$ のグラフと $x$ 軸、$y$ 軸で囲まれた図形の面積
とするとき、
$S_1=S_2$ となるときの $m$ の値を求め、$y=f(x)$, $y=S(x)$ のグラフを書け。
$f(x)$ のグラフはすぐに書けます。また、$f(x)$ と $S(x)$ は微分と積分の関係にあります。つまり、$S(x)$ のグラフを書こうと思えば、$f(x)$ のグラフ(増減表)が分かればよいです(もう分かっている)。増減表のグラフ版のようなもので、次のアニメーションのイメージです。
赤が $S(x)$ で、その微分である $f(x)$ が青。青の値が0になるところで、赤のグラフは極値を持ちます。
$S_1=S_2$ とは、$S(m)=0$ ということです。というのも、$S(m)$ は $f(x)$ と $x$ 軸との $0$~$m$ の面積なので $\left(S(m)=\int_0^mf(t)\,dt\right)$、$0\le x\le 1$ の面積 $S_1$ と $1\le x\le m$ の面積 $S_2$ が同じになるところとは、
$S(m)=S_1+(-S_2)=0$ となるところ
です。実際の共通テストでは誘導が長いですが、このイメージが持てればとてもシンプルです。
解. $S_1=S_2$ となる $m$ を求め、$f(x)$ と $S(x)$ の関係を確認する
$S_1=S_2$ のとき、
$$S(m)=0$$
よって、
\[ \begin{aligned} S(m) &= \int_0^m f(t)\, dt \\ &= \int_0^m 3(t-1)(t-m)\, dt \\ &= \frac{1}{2}m^2(3-m) \end{aligned} \]
WolframAlphaで確認。
$m>1$ で 0 になるのは、
$$m=3$$
このときのグラフは次の通り。

IIB:第5問 ベクトル方程式
この問題では「ベクトル方程式」を使います。
最短距離とくれば垂直を発想しましょう。
点 $\mathrm{O}$ を原点とする座標空間に4点 $\mathrm{A}(2,7,-1)$, $\mathrm{B}(3,6,0)$, $\mathrm{C}(-8,10,-3)$, $\mathrm{D}(-9,8,-4)$ がある。
- $\mathrm{A}$, $\mathrm{B}$ を通る直線を $l_1$ とし点 $\mathrm{P}$ がこの上を、
- $\mathrm{C}$, $\mathrm{D}$ を通る直線を $l_2$ とし点 $\mathrm{Q}$ がこの上を動く。
このとき、線分 $\mathrm{PQ}$ の長さが最小になるときの $\mathrm{P}$, $\mathrm{Q}$ の座標を求めよ。
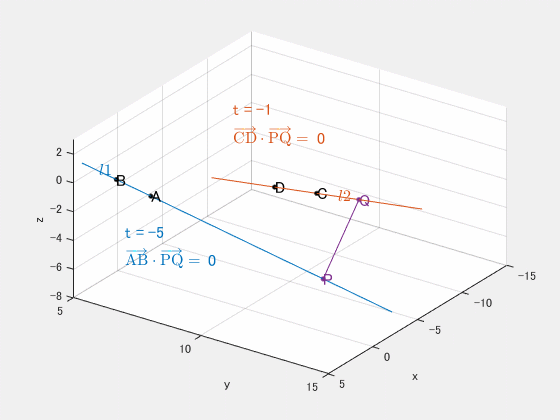
「長さが最小 $\iff$ 垂直」のイメージ:
最短距離になるとき、$\overrightarrow{\mathrm{PQ}}$ は
両直線の方向ベクトルに垂直
つまり、
\[ \begin{aligned} \overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{PQ}} &= 0\\ \overrightarrow{\mathrm{CD}}\cdot\overrightarrow{\mathrm{PQ}} &= 0 \end{aligned} \]
この 2 つを満たすようにパラメータを決めます。
解. 2直線の最短距離となる点P,Qの座標を求める
直線 $l_1$, $l_2$ のベクトル方程式:
\[ \begin{aligned} l_1:\quad \overrightarrow{\mathrm{OP}} &= \overrightarrow{\mathrm{OA}} + s\,\overrightarrow{\mathrm{AB}}\\ l_2:\quad \overrightarrow{\mathrm{OQ}} &= \overrightarrow{\mathrm{OC}} + t\,\overrightarrow{\mathrm{CD}} \end{aligned} \tag{1}\label{eq1} \]
より、
\[ \begin{aligned}\overrightarrow{\mathrm{PQ}} &= \overrightarrow{\mathrm{OQ}} \,- \overrightarrow{\mathrm{OP}}\\ &= \overrightarrow{\mathrm{AC}} \,- s\,\overrightarrow{\mathrm{AB}} + t\,\overrightarrow{\mathrm{CD}}\end{aligned} \]
最短距離の条件より、
\[ \overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{PQ}} = -15 – 3s=0\\\overrightarrow{\mathrm{CD}}\cdot\overrightarrow{\mathrm{PQ}} = 6 + 6t=0 \]
よって、
\[ s=-5,\quad t=-1\]
これを式\eqref{eq1}に代入すると、
$\mathrm{P}(-3,\,12,\,-6)$
$\mathrm{Q}(-7,\,12,\,-2)$
まとめ
共通テストの数学は、丁寧な誘導に乗れば確実に得点できるように作られています。まずは誘導の流れに素直に従い、前半の取りやすい部分をしっかり得点することが大切です。
一方で、復習の段階では「誘導なしでどこまで見通しを立てられるか」を意識すると、理解が一段深まります。本ページではそのために、あえて誘導を省き、本質に立ち返って考える練習ができるように構成しています。
平方根・メネラウス・整式の割り算・微積・ベクトルという典型分野を通して、“なぜそうなるのか” を自分でつかむ力を養うことができます。繰り返し解くことで、誘導がなくても自然と見通しが立つようになり、次の問題への自信にもつながります。
この記事が、あなたの理解を支え、学習の土台をより強くする一助になれば嬉しいです。





コメント