微分を習ったとき、「なぜ接線の傾きになるの?」と疑問に感じたことはありませんか。そこでこの記事では、「微分=超拡大したときの傾き」というイメージをアニメーションを通じてつかむことを目的にします。limやdx,dyといった記号の “気持ち” も自然に理解できるようになります。
微分の定義とイメージ:曲線を超拡大すると直線になる
微分の定義式を確認する
例として $f(x)=x^2$ を $x=1$ で微分します。定義式は次の通りです。
$$f^{\prime}(1) = \lim_{h\to 0}\frac{f(1+h)-f(1)}{h}\tag{1}\label{p7eq1}$$
しかし、この式はとっつきにくく、式変形を理解しても実感がわきにくいものです。
定義式だけでは直感的に分かりにくい理由
定義式は「何をしているのか」が見えにくいため、ここではアニメーションを使って 式の気持ち を理解します。
アニメーションで見る「微分の正体」
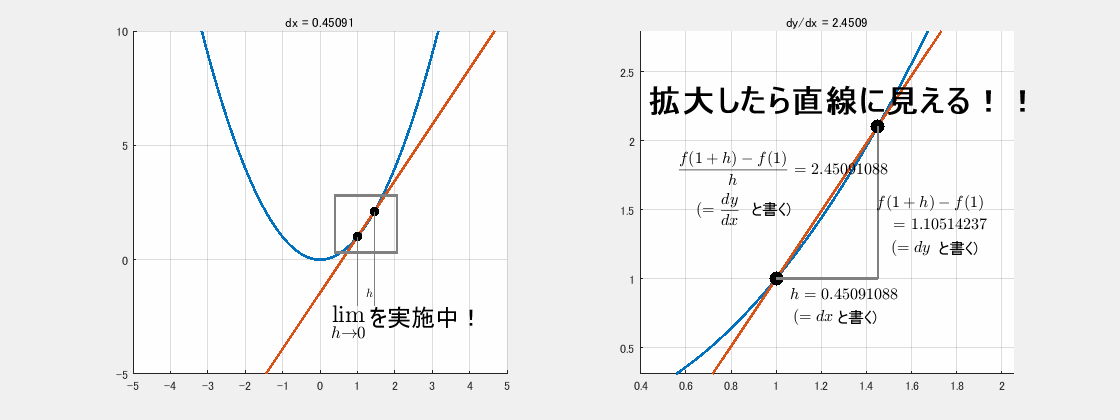
超拡大すると曲線が直線に見える
アニメーションでは、$y=x^2$ の $x=1$ 付近をどんどん拡大します。
すると、曲線だったはずのグラフがほぼ直線に見えてきます。
つまり、
- 曲線も、十分に狭い範囲を見れば直線に見える。
- その直線の傾きこそが微分係数。
ということです。
微分係数=ミクロで見たときの傾き
超拡大したとき、青線(元の曲線)と赤線(接線)がほぼ一致します。これが「微分=接線の傾き」の正体です。
$ \lim$ と「超拡大」の関係
$h$ を小さくする操作が $\lim$ の正体
アニメーションでは、最初に $h=1$ のような大きめの幅から始め、徐々に $h$ を小さくしています。これは定義式の
$$\lim_{h\to 0}$$
を視覚的に表現したものです。
$h\to 0$ が「接線」に近づく理由
- $h$ が大きい → 曲線の形がよく見える(下図の上)
- $h$ が小さい → 直線に近づく(下図の下)
- $h\to 0$ → 完全に直線に見える(=接線)
この流れがそのまま「微分のイメージ」です。


$dx$, $dy$ の気持ち:分数としての微分
$h$ が極小になると $dx$ と呼びたくなる
アニメーションの後半では、横幅 $h$ を $dx$、縦幅 $f(1+h)-f(1)$ を $dy$ と書き換えています。これは、
- $h$ が極端に小さいとき → $dx$ と呼びたくなる
- その時の縦の変化量 → $dy$
という “気持ち” を表しています。
$dy/dx$ は傾きに見える
$$\frac{dy}{dx}$$
はまさに「縦の変化量$\div$横の変化量」=傾き として自然に理解できます。
例:$y=x^2$ を実際に微分してみる
定義式を使った計算
アニメーションで見た直感を、定義式で確かめます。
\begin{eqnarray}
f^\prime(1) &=& \lim_{h\to 0}\frac{(1+h)^2-1^2}{h}\\
&=& \lim_{h\to 0}\frac{2h+h^2}{h}\\
&=& \lim_{h\to 0}(2+h)\\
&& =2
\end{eqnarray}
アニメーションで見た「傾き $2$」と一致します。
アニメーションの結果と一致する理由
超拡大したときの直線の傾きが $2$ に見えたのは、定義式の極限計算と完全に対応しています。
一般化:任意の $x$ での傾きを求める
導関数 $f^\prime(x)=2x$ の導出
同じ計算を $x$ のままで行うと、
$$f^\prime(x)=2x$$
となります。これが $y=x^2$ の導関数です。
\begin{eqnarray}
f^\prime(x) &=& \lim_{h\to 0}\frac{(x+h)^2-x^2}{h}\\
&=& \lim_{h\to 0}\frac{2xh+h^2}{h}\\
&=& \lim_{h\to 0}(2x+h)\\
&& =2x
\end{eqnarray}
$x^n$ の微分公式
さらに一般化すると、
$$(x^n)^\prime = nx^{n-1}$$
となります。これは「面倒な定義式の計算をしなくてもよい」という便利な公式です。
$\lim$ の気持ち:「おおよそ」で考える
$h$ が小さいときは無視できるという感覚
$$\lim_{h\to 0}(x+h)=x$$
は、
- $h$ は十分小さい
- だから「ほぼ $x$」とみなしてよい
という “おおよそ” の感覚を表しています。
「超拡大=おおよそ直線」の世界
微分の「曲線を拡大したら直線に見える」というイメージも、
この「おおよそ直線でいいよね」という感覚と同じです。
まとめ:微分とは “ミクロの世界の傾き”
- 曲線も、ミクロに見れば直線に見える
- その直線の傾きが微分係数
- $dx$, $dy$ は極小の変化量
- $\lim$ は「近づける」という操作
- 微分公式は、この直感の上に成り立っている
地球を例にすると分かりやすいです。
地球は丸いのに、私たちの足元は平面に見えますよね。
微分とは、まさにミクロの世界で見たときの姿を扱う操作なのです。


コメント