本記事では、典型的な軌跡の形を具体的な例を交えて解説し、理解を深めるヒントを紹介します。入試問題としても頻出のテーマなので、ぜひチェックしてみてください！
$|z-3i|=5$：円
$|z-3i|$ は、$z$ と $3i$ との距離を表します。$3i$ は複素数平面上で $(0,3)$ なので、その点との距離が $5$ であるということは、
点 $(0,3)$ を中心とする半径 $5$ の円
を表します。
$|z-3i|=|z-5|$：垂直二等分線
$|z-3i|$ は、$z$ と $3i$ との距離を表します。つまり、点 $(0,3)$ からの距離です。同様に、$|z-5|$ は、$z$ と$5$ との距離です。つまり、点 $(5,0)$ からの距離です。
これらが等しいと言っているので、
点 $(0,3)$ からの距離と点 $(5,0)$ からの距離が等しい点の集合
つまり、
点 $(0,3)$ と点 $(5,0)$ の垂直二等分線
を表します。
$ 2|z-1|=|z+2|$：円
両辺を2乗する
両辺を2乗して整理すると、
\begin{eqnarray}
&&(2|z-1|)^2 = |z+2|^2\\
&&4(z-1)\overline{(z-1)} = (z+2)\overline{(z+2)}\\
&&4(z-1)(\overline{z}-1) = (z+2)(\overline{z}+2)\\
&&4z\overline{z}-4z-4\overline{z}+4= z\overline{z}+2z+2\overline{z}+4\\
&&3z\overline{z}-6z-6\overline{z}=0\\
&&z\overline{z}-2z-2\overline{z}=0\\
&&(z-2)\overline{(z-2)}=4\\
&&|z-2|^2=4\\
&&|z-2|=2
\end{eqnarray}
となりますからすなわち、点 $(2,0)$ を中心とする半径 $2$ の円を表します。
図形的に考える
$2|z-1|=|z+2|$ は、
$$|z-1|:|z+2|=1:2$$
と書けます。このように書くと元の式の意味は、
点 $(1,0)$ と点 $(-2,0)$ からの距離が $1:2$ である点の集合
ということになります。これはアポロニウスの円と呼ばれる有名な軌跡で、
線分を内分する点と外分する点を直径の両端とする円
になります。
ちょっとひっかけ？ $|iz+3|=|z-5|$
これは $z$ に係数がついているところからすると、ここと類似かと思い、円になると思いそうです。
しかしこれはむしろこちらと類似で垂直二等分線になります。というのも、
$$|iz+3|=|i(z-3i)|=|i||z-3i|=|z-3i|\quad (\because |i|=1)$$
となるので元の式は、
$$|z-3i|=|z-5|$$
となり、「こちらと類似」というよりは全く同じになります。
入試問題より
慶応義塾大学・理工学部＠25年度
複素数平面上で、方程式 $|z+i|=2|z-\sqrt{3}|$ を満たす点 $z$ 全体が表す図形は、中心が[ ]、半径が[ ]の円である。
解答
$$|z+i|:|z-\sqrt{3}|=2:1$$
より、求める図形は点 $\mathrm{A}(0,-1)$, 点 $\mathrm{B}(\sqrt{3},0)$ を $2:1$ に内分する点 $\mathrm{C}(\displaystyle\frac{2\sqrt{3}}{3},-\displaystyle\frac{1}{3})$, 及び外分する点 $\mathrm{D}(2\sqrt{3},1)$ を直径とする円となるから、
中心：$(\displaystyle\frac{4\sqrt{3}}{3},\displaystyle\frac{1}{3})$
半径：$\displaystyle\frac{4}{3}$
の円。
これの別解や、また他の問題を下記↓にまとめました。こちらでじっくりと取り組んでください。
まとめ
複素数平面の軌跡問題の基本になる部分を解説しました。図形的に理解できるものは図形的に理解する方が圧倒的に楽です。しかし、図形的な発想にたどり着かない場合でも計算で何とかなる場合も多いですので、両方の解き方を練習するとよいです。
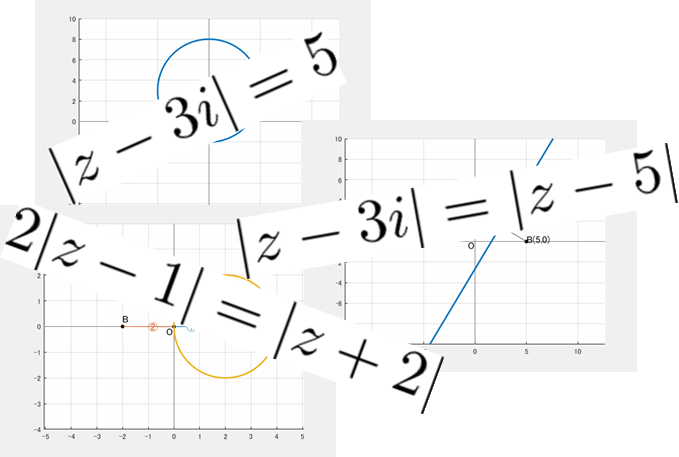
コメント