積分とは「微小な量を足し合わせる操作」です。そう聞くと何となくイメージはできても、実際に “何をどう積み重ねているのか” がつかみにくい人は多いはず。特に、
「なぜ円周を積分すると面積になるのか?」
「球の表面積を積分すると体積になるのはどうして?」
といった疑問は、公式として覚えていても直感的に理解しづらいポイントです。
この記事では、積分の本質を “微小な短冊や薄い皮を足し合わせるイメージ” として捉えながら、
短冊の積分 → 円周から面積 → 球の表面積から体積 → 物理への応用
という流れで、積分の意味を丁寧に解説します。
積分が「ただの計算」ではなく、図形や物理の仕組みを理解するための強力な道具であることが、自然と見えてくるはずです。
積分は「微小な量の足し合わせ」
短冊で考える積分の基本イメージ
積分とは、微小な量を足し合わせる操作です。まずはそのイメージをつかむためにシンプルな例として
$f(x)=x^2$ を $0$~$1$ で積分する場合
を例に考えてみます。定積分の計算は次のようになります。
$$\int_0^1 x^2\,dx = \frac{1}{3}\left[x^3\right]_0^1 = \frac{1}{3}\tag{1}\label{eq1}$$
しかし、重要なのは この式が何を意味しているのか という点です。そのイメージを、教科書的な視点と、より実践的な視点の2つから見ていきます。
教科書的な視点(幅 $h\to dx$ の話)
教科書では、短冊の幅 $h$ をどんどん小さくし、
$$\lim_{h\to 0}$$
とすることで積分を定義します。幅 $h$ が限りなくゼロに近づくと、「もうこれは $dx$ と書きたい」という気持ちになります。微分の時と同じ感覚です(参考:【微分とは何か?】)。
実践的な視点(限りなく薄い短冊の敷き詰め)
次に、より実践的なイメージです。限りなく薄い短冊(幅 $dx$)を敷き詰めていくと考えます。各短冊の面積は、
- 横幅:$dx$
- 縦の長さ:その位置での $x^2$
なので、例えば
$$0.50^2\,dx,\quad 0.51^2\,dx,\quad\cdots$$
のような短冊が並びます。
それらを全部足し合わせると、
$\begin{eqnarray}
S&=&0^2dx+0.01^2dx+\cdots\\
&+&0.50^2dx+0.51^2dx+\cdots\\
&+&0.98^2dx+0.99^2dx\tag{2}\label{eq2}
\end{eqnarray}$
となります。説明のために $dx=0.01$ としていますが、実際には 限りなくゼロに近い幅 です。その極限を記号で表したものが積分記号 $\int$ であり、
$$\int_0^1x^2\,dx$$
は、
$x^2\,dx$ を $0$ から $1$ まで足したもの
という意味になります。

短冊以外にもある積分のイメージ
積分の本質は 微小な量の足し合わせ ですが、これは短冊だけに限りません。短冊以外の他の図形や体積にも同じ考え方を応用できます。
円周を積分したら面積になる理由
円周は $2\pi r$、円の面積は $\pi r^2$ 。
この2つが微分積分の関係にあるのは偶然ではありません。
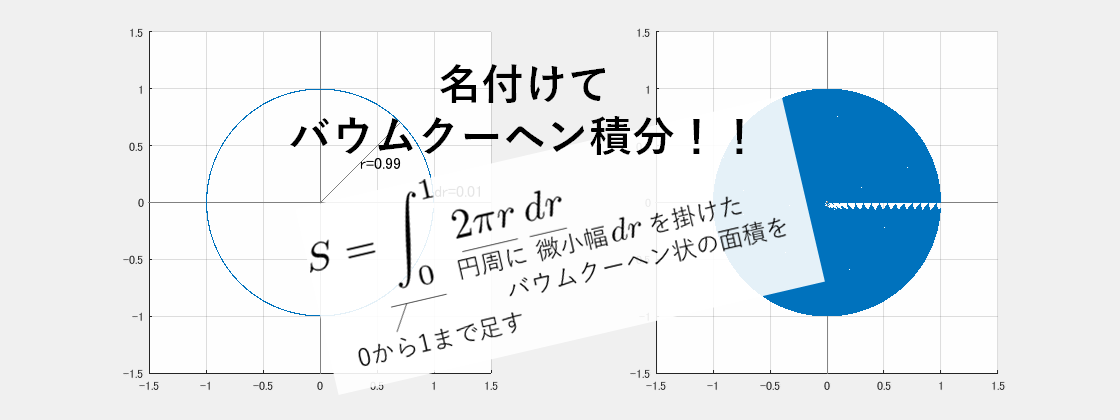
円を「薄い皮(幅 $dr$)」として外側へ巻き付けていくイメージを考えます。バウムクーヘンの層を重ねるような感覚です。
半径 $r$ の位置での薄皮の長さは円周 $2\pi r$。
それに幅 $dr$ を掛けたものが、その薄皮の面積 $dS$ です。
$$dS=2\pi r\,dr$$
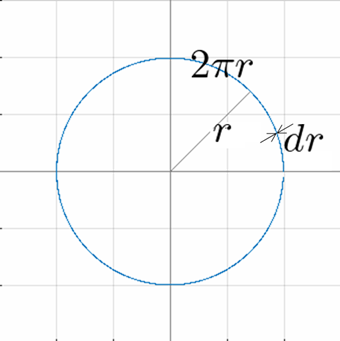
これを積分すると、
$$S=\int_0^1 2\pi r\,dr=\pi$$
となり、確かに円の面積が得られます。

球の表面積を積分すると体積になる理由
球の表面積は $4\pi r^2$、体積は $\displaystyle\frac{4}{3}\pi r^3$。
これも積分でつながっています。
今度は「薄い殻(幅 $dr$)」を重ねていくイメージです。りんご飴の表面に薄い層を塗り重ねるような感覚です。
$$V=\int_0^r 4\pi r^2\,dr=\frac{4}{3}\pi r^3$$
となり、球の体積が得られます。

円の面積を三角形の和として理解する(ダメ押し)
積分のイメージがつかめていれば、円の面積を「三角形の寄せ集め」として捉えることもできます。
円を細かい扇形に分けると、底辺が $r\,d\theta$、高さが $r$ の三角形になります。その面積は、
$$dS = \frac{1}{2}r^2\,d\theta$$

これを $\theta=0$ から $2\pi$ まで足し合わせれば、
$$S=\frac{1}{2}r^2\int_0^{2\pi}\,d\theta=\pi r^2$$
となります。

左の図は上の図(動画)の左側の□部分であり、拡大図です。□があまりにも小さくて線にしか見えませんが。なお、拡大図は見やすいように縦横比は等しくなく、崩しています。
これは、図のように細かい三角形を寄せてきて大きな三角形にした、とみることもできます。

積分は物理でどう使われているか
積分の「微小な量を足し合わせる」という考え方は、物理で頻繁に登場します。
速度を積分すると変位
ある時刻 $t$ の速度を $v(t)$ とすると、微小時間 $dt$ の間に進む距離は
$$dx=v(t)\,dt$$
です。この「微小時間では速度が一定とみなせる」という考え方が、まさに積分の短冊イメージです。
等速度運動
速度が一定 $v_0$ の場合、
$$x=\int_0^t v_0\,dt=v_0t$$
これは、長方形の面積そのものです。

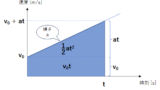
等加速度運動
速度が直線的に増える場合、
$$x=\int_0^t(v_0+at)\,dt=v_0t+\frac{1}{2}at^2$$
これは台形の面積に対応します。

参考記事:等加速度運動の3公式
力を積分すると仕事(位置エネルギー)
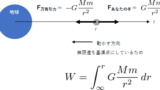
万有引力に逆らって物体を動かすとき、外力が行った仕事は、
$$dW=G\frac{Mm}{r^2}\,dr$$
これを無限遠から $r$ まで積分すると、
$$W=-G\frac{Mm}{r}$$
となり、位置エネルギーが得られます。
参考:力学的エネルギー保存の法則
ロケット方程式・シミュレーションへの応用
ロケットの推進や、空気抵抗・スピンを含むボールの軌道計算でも、時間を細かく区切って積分を行います。
詳しい式の導出はリンク先で解説していますが、ここでは「積分=微小な量の足し合わせ」がシミュレーションの基礎になっていることだけ押さえておけば充分です。

まとめ:積分は「微小な量の足し合わせ」
積分の本質は、「微小な量を足し合わせる」というシンプルな考えです。
- 短冊を足し合わせる
- 薄皮を重ねる
- 三角形を並べる
といったイメージを通して、円周と面積、表面積と体積の関係が自然に理解できます。
さらに物理では、
速度→変位、力→仕事
など、積分の考え方があらゆる場面で登場します。
このイメージを持っておくことで、積分は単なる計算問題ではなく、
世界の仕組みを理解するための強力な道具
になります。
ぜひ、この積分のイメージを自分のものにしてください。




コメント