接線がある点を通るかどうか──これは大学入試で頻出のテーマですが、
実は「逆像法」を使えば一瞬で判断できます。
今回扱うのは、実際の入試問題の(1)にあたる基礎部分だけです。
とはいえ、この(1)をスラスラ処理できるかどうかが、
後続の(2)(3)でつまずかないための鍵になります。
この記事では、逆像法の典型パターンを大学入試問題を通して確認しながら、
接線の“解の存在”をどう見抜くか、その発想の流れを整理します。
逆像法の本質はこちらで詳しく解説しています。
また、順像法との比較や使い分けはこちら。
慶応義塾大学・理工学部(25年度)
曲線 $\mathrm{C}\,:\,y=\displaystyle\frac{1}{x-4}$ $(x>4)$ の接線で
点 $\mathrm{Q}(1,-1)$ を通るものは存在しないことを証明せよ。
問題②(1)のみを抽出
この問題↑を見たとき、「あ、逆像法の形だな」と気づけると強いです。
先ほどの記事↓で扱った発想がそのまま使えます。
接線の式 ($t$ の関数) が点 $\mathrm{Q}$ を通ると仮定し、$t$ に解があるかどうかを調べる──これが逆像法の基本です。
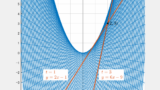
イメージはこんな感じ↓。
この図を見ると、接線が $\mathrm{Q}$ を通りそうにないことが直感的に分かります。
解1. 逆像法:そこに解はあるんか?
曲線 $ \mathrm{C} $ 上の点 $ (t, \displaystyle\frac{1}{t-4}) $ $(t>4)$ における接線の方程式は
$$y = -\frac{1}{(t-4)^2}(x-t) + \frac{1}{t-4} \tag{1}\label{p7415eq1}$$
この接線が点 $\mathrm{Q}(1,-1)$ を通るかどうかを調べます。
つまり、接線が $\mathrm{Q}$ を通ると仮定して $t$ を求めてみるわけです。
その $t$ が“存在するかどうか”が勝負どころです。
$$-1=-\frac{1}{(t-4)^2}(1-t)+\frac{1}{t-4}$$
$$-(t-4)^2=-(1-t)+(t-4)$$
$$t^2+6t+11=0$$
判別式を $D$ として、
\begin{eqnarray}
\frac{D}{4} &=& 3^2-11\\
&=&-2<0
\end{eqnarray}
判別式が負になるため、$t$ に解は存在しません。
よって、接線は存在しない。
接線の方程式 \eqref{p7415eq1} について
接線の式 \eqref{p7415eq1} はサッと書きましたが、これは以下の記事の「一行で接線を書くコツ」を使っています。
解2. 平行移動で見通しをよくする
$x$ 軸方向に $-4$ 平行移動すると、曲線は $ y=\displaystyle\frac{1}{x} $ に変わり、計算がシンプルになります。
平行移動後の問題は、
曲線 $\mathrm{C^\prime}\,:\,y=\displaystyle\frac{1}{x}$ $(x>0)$ の接線で
点 $\mathrm{Q^\prime}(-3,-1)$ を通るものは存在しないことを証明せよ。
という形になります。
あとは同じ手順で、$t$ に解がないことを示すだけです。
曲線 $\mathrm{C^\prime}$ 上の点 $(t,\,\displaystyle\frac{1}{t})$ $(t>0)$ における接線の方程式は
$$y=-\frac{1}{t^2}(x-t)+\frac{1}{t}$$
この接線が点 $\mathrm{Q^\prime}(-3,-1)$ を通ることがあるかどうかを調べればよい。
すなわち $(-3,-1)$ を代入した式
$$-1=-\frac{1}{t^2}(-3-t)+\frac{1}{t}$$
が $t$ について解を持つかどうかを調べればよい。
これを $t$ について整理すると、
$$-t^2=-(-3-t)+t$$
$$t^2+2t+3=0$$
判別式を $D$ として、
\begin{eqnarray}
\frac{D}{4} &=& 1^2-3\\
&=&-2<0
\end{eqnarray}
よって、接線は存在しない。
まとめ
大学入試問題を題材に、逆像法の基本を確認しました。
今回扱ったのは(1)にあたる基礎部分だけですが、
ここをスラスラ処理できるかどうかが、
後続の(2)(3)でつまずかないための鍵になります。
逆像法の本質はこちらで詳しく解説しています。




コメント