運動量保存の法則を「運動方程式」でなぞる｜同じ答えになる理由を”問題で”腹落ち！

　運動量保存の法則と運動方程式の両方で同じ問題を解き、本当に同じ結果になることを確かめます。さらに、なぜ同じになるのかを運動方程式の積分という視点から眺め直してみます。解く問題のイメージは↓の動画の通りです。この問題の諸元は問題の諸元にまとめています。

　ここでは「なぜ同じになるのか」を解説しますが、運動量保存の法則そのものの導出は↓の記事でじっくり扱っています。あわせて読むと完全に腹落ちするはずです。

問題設定

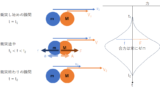
状況としては、下の台車だけが $t=0$ にハンマーでガツンと叩かれて急に速度を持ったようなイメージです。台車と物体の間には摩擦があるので、運動は次のように進みます。

• 物体は台車に引きずられて動き出し
• しばらくは滑りながら相対運動をし
• やがて台車と同じ速度になり、一体となって動く

解1. 運動量保存の法則で解く

まずは運動量保存の法則を使って、最終速度 $v_1$ を一気に求めてみます。
外力が働かない水平方向について、衝突（相互作用）前後で運動量の和は一定なので、

$$Mv_0 + m\cdot 0 = (M+m)v_1$$

よって、

$$v_1=\frac{M}{M+m}\, v_0$$

これが運動量保存の法則を使った答えです。とてもコンパクトに求まりますが、「なぜこれでよいのか」を運動方程式から確かめていきます。

解2. 運動方程式で解く

次に、物体と台車それぞれに働く力を整理し、運動方程式から同じ結果が出ることを確認します。
物体が台車上で滑っている間の力の様子は下図のようになります。

とすると、物体と台車の運動方程式は次のようになります。

物体 $m$ の運動方程式：

\begin{eqnarray}
\left\{ \begin{array}{l}
ma =\mu N_1\\
0 = N_1 – mg\tag{1}\label{p1232eq1}
\end{array}
\right.
\end{eqnarray}

台車 $M$ の運動方程式：

$$MA=-\mu N_1\tag{2}\label{p1232eq2}$$

式\eqref{p1232eq1} より、

$$a=\frac{\mu N_1}{m}=\frac{\mu mg}{m}=\mu g$$

物体 $m$ はこの加速度で加速して、初速度 $0$ から速度 $v_m$ を持つようになるので、$t$ 秒後の速度 $v_m$ は

$$v_m = at = \mu g t\tag{3}\label{p1232eq3}$$

　一方、式\eqref{p1232eq2} より

$$A=-\frac{\mu N_1}{M}=-\frac{\mu mg}{M}$$

台車 $M$ はこの加速度で減速し、初速度 $v_0$ から速度 $v_M$ を持つようになるので、$t$ 秒後の速度 $v_M$ は

$$v_M = v_0+At = v_0-\frac{\mu mg}{M}\, t\tag{4}\label{p1232eq4}$$

物体と台車の速度が等しくなった瞬間に摩擦力はゼロとなり、それ以降は同じ速度で動き続けます。この時刻を $t_1$ とすると、$v_M=v_m(=v_1)$ なので、式\eqref{p1232eq3}, \eqref{p1232eq4} より

\begin{eqnarray}
\begin{array}{c}
\mu gt_1=v_0-\displaystyle\frac{\mu mg}{M}\, t_1\\
\therefore\;t_1=\displaystyle\frac{M}{\mu (M+m)g}\, v_0
\end{array}
\end{eqnarray}

このときの速度 $v_1$ は式\eqref{p1232eq3} を使うと、

\begin{eqnarray}
v_1&=&\cancel{\mu}\cancel{g}\frac{M}{\cancel{\mu}(M+m)\cancel{g}}\, v_0\\
&=&\frac{M}{M+m}\, v_0
\end{eqnarray}

解1と同じ結果が得られました。ここまでは「愚直に運動方程式を解いた」だけですが、次にこれが運動量保存の法則とどう結びついているかを見ていきます。

解説. 運動量保存の法則も結局は運動方程式を解いている

ここからは、解2で立てた運動方程式から、解1の「運動量保存の法則」がどのように現れてくるかをなぞってみます。より一般的な導出や、外力ゼロの運動方程式との関係は↓の記事で詳しく扱っています。

解1の復習：運動量保存の法則の導出をなぞる

解2で立てた横方向の運動方程式だけを取り出すと、

\begin{eqnarray}
\left\{ \begin{array}{l}
ma &=& \mu N_1\\
MA &=& -\mu N_1
\end{array}
\right.
\end{eqnarray}

上下の式を足し合わせると、

$$ma+MA = 0\tag{5}\label{p1232eq5}$$

これを $t=0$ から $t=t_1$ まで積分すると、

\begin{eqnarray}
\begin{array}{c}
\displaystyle m\int_0^{t_1}a\, dt + M\int_0^{t_1}A\, dt = 0\\
\displaystyle m\int_0^{t_1}\frac{dv}{dt}\, dt + M\int_0^{t_1}\frac{dV}{dt}\, dt = 0\\
\displaystyle m\int_0^{v_1}dv + M\int_{v_0}^{v_1}dV = 0
\end{array}
\end{eqnarray}

$$ m(v_1-0) + M(v_1-v_0) = 0\tag{6}\label{eq6}$$

これはまさに解1で使った運動量保存の式そのものです。つまり、運動量保存の法則は「外力ゼロの運動系における運動方程式を時間で積分した結果」に他なりません。

解2と解1を結び付ける：途中の時刻でも成り立つ関係

式\eqref{p1232eq5} を任意の時刻 $t$ まで積分

式\eqref{p1232eq5} を、任意の時刻 $t(>0)$ まで積分した形で書くと、

$$m\int_0^{t}a\, dt + M\int_0^{t}A\, dt = 0$$

時刻 $t$ での速度を $v_m$, $v_M$ と書くと、

$$m(v_m-0) + M(v_M-v_0) = 0\tag{7}\label{p1232eq7}$$

これは式\eqref{eq6}の $v_1$ を $v_m$, $v_M$ にしただけにはなりますが、「任意の時刻 $t$ において、物体と台車の運動量の変化の和がゼロである」という関係を表しています。

具体的時刻 $t=0.5$ での例

例えば $t=0.5$ のとき、

• 台車の速度は $5$ から $4.4$ に変化しており ($dv=\,$$-0.6$)、
• 物体の速度は $0$ から $1$ に変化しています。($dV=\,$$1$)

質量 $(M=10,\, m=6)$ を掛けると、それぞれの運動量の変化は

• $M\,dV=10\times\,$$(-0.6)$$\,=\,$$-6$
• $m\,dv=6\times\,$$1$$\,=\,$$6$

となり、

$m(v_m-0) + M(v_M-v_0) = 0\tag{7再掲}$
$6$$\,+\,$$(-6)$$\,=0$

が確かに成り立っています。

任意の時刻でも同様

他の時刻でも同様で、常に式\eqref{p1232eq7} の関係が成り立っています。外力が働かない限り、いつでもこの式が成り立つというのが、運動量保存の法則が主張していることです。

$v_m=v_M=v_1$ となったとき

特に、$v_m=v_M=\,$$v_1$ となったときにも式\eqref{p1232eq7} は成り立っているので、

$m(\,$$v_1$$\,-0) + M(\,$$v_1$$\,-v_0) = 0$

から $v_1$ を求めるのが「運動量保存の法則で解く」というやり方だ、というわけです。この式は2物体の速度の関係を一気に求めるには非常に便利ですが、各時刻での速度そのものは分かりません。

つまり、解2では任意の時刻 $t$ での速度が求まり、解1は最終速度だけが求まる

つまり、

• 解2：任意の時刻 $t$ での速度が求まる
• 解1：最終速度だけが求まる

です。任意の時刻 $t$ での速度を知りたければ、

解2のように式\eqref{p1232eq1}, \eqref{p1232eq2} から加速度を求めて時間で積分

しかし今回のように「最終速度 $v_1$ だけ分かればよい」場合は、

解1のように式\eqref{p1232eq1}, \eqref{p1232eq2} を足して余分な $\mu N_1$ を消して積分

した運動量保存の法則を使う方が、はるかにスマートに解けるわけです。

まとめ：解1も解2も「外力ゼロの運動方程式」を解いているだけ

以上のように、

• 解2のように \eqref{p1232eq1}, \eqref{p1232eq2} から加速度を求めて時間で積分する方法でも、
• 解1のように \eqref{p1232eq1}, \eqref{p1232eq2} を足して外力ゼロの性質を使い、余分な項を消してから積分する方法でも、

どちらも本質的には

「外力ゼロの運動方程式」を解いている

ことに変わりはありません。

運動量保存の法則は、一見すると「新しい法則」のように見えますが、外力が働かない系における運動方程式を時間で積分した結果に過ぎません。そのことが分かると、本質は運動方程式であり、状況に応じて解きやすい方を選べばよいだけだと分かり、気が楽になります。

運動量保存の法則そのものの導出や力積とのつながりについては↓の記事で詳しく解説しています。今回の問題とあわせて読むことで、理解が “線” ではなく “面” になります。

問題の諸元

冒頭の動画で用いたパラメータは次の通りです。

• $M=10$ [kg]
• $m=6$ [kg]
• $\mu=0.2$
• $v_0=5$ [m/s]
• $g=9.8$ [m/s$^2$]

このときの最終的な速度 $v_1$ は、

$$v_1 = \frac{M}{M+m}\, v_0 = \frac{10}{10+6}\times 5 = 3.125\;\mathrm{[m/s]}$$

また、速度がそろう時刻 $t_1$ は、

$$t_1 = \frac{M}{\mu (M+m)g}\, v_0 = \frac{10}{0.2\times (10+6)\times 9.8}\times 5 = 1.594\;\mathrm{[s]}$$

シミュレーションではさらに、

• $dt=0.01$ [s]

という時間刻みを設定しています。冒頭の動画で最終速度が $3.125$ からわずかにずれているのは、この $dt$ が有限だからです。$dt$ を $0.00001$ に小さくすると、有効数字3桁では $3.125$ に一致しました。

この $dt$ の話からも分かるように、積分は「細かい短冊の寄せ集め」として理解できます。$dt=0.01$ でもかなり良い近似になりますが、完全ではありません。$dt$ を小さくすればするほど真の値に近づき、極限としての積分では「無限に細かい短冊の和」を取ることで、正確な値が得られます。

積分を「細かい短冊の寄せ集め」としてイメージする話は↓の記事でも扱っています。円の面積 $\pi r^2$ と円周の長さ $2\pi r$ が微分積分の関係であることが、すっきりと理解できるはずです。