【テニスの物理】最適なラケットの重さは？ 6倍の定理

　テクニカルテニスという本を読んでいるとラケットの重さはボールの重さの6倍であるとの記述がありました¹。確かにテニスボールの重さは57gでラケットの重さはその6倍の342g程度です。他の競技も同様に、野球ではボールの重さは145gでバットの重さは900g程度ですし、サッカーボールの重さは430gで片足の重さは2500g程度です。

少し調べたところ、「知って得する身近なScience バットの重さ ラケットの重さ」という記事があり、このことを理論的に述べています。ここではこの記事を元に少しアレンジして記載します。具体的には上記の参考文献ではエネルギー保存の法則を使っているのに対し、こちらでは跳ね返り係数の式を使います。そして両者が同じになることを見てもらえると、それはそれで一つ知識になるかなと思います。

問題の整理

　ここでは左側に打つため、左側を正の向きとして設定します。このとき相手が打った球の符号は負なので $-v_1$ と置きました。こう置くことで $v_1$ 自体の符号を正とすることができます。

立式

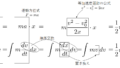
　運動量保存の法則と跳ね返り係数の式を立てます。

$$\begin{eqnarray} \left\{\begin{array}{l} -mv_1+MV_1=mv_2+MV_2\tag{1}\label{p2952eq1}\\ e = -\displaystyle\frac{v_2-V_2}{-v_1-V_1} \end{array} \right. \end{eqnarray}$$

計算の目的はボールとラケットの最適な重さの比を出すことなので、$\eqref{p2952eq1}$の上の式の両辺を $m$ で割り、その比 $\displaystyle\frac{M}{m}$ の値を $x$ と置きます。すると、

$$\begin{eqnarray} \left\{\begin{array}{l} -v_1+xV_1=v_2+xV_2\tag{2}\label{p2952eq2}\\ e = -\displaystyle\frac{v_2-V_2}{-v_1-V_1} \end{array} \right. \end{eqnarray}$$

となります。これを $v_2$, $V_2$ で解けばよいことになります。

計算

　式$\eqref{p2952eq2}$は未知数が $v_2$, $V_2$ の二つで式も二つあるので解くことができます。腕試しに解いてみるのもいいと思います。ここではWolfram Alphaに任せてしまいます。するとその解は、

$$\begin{eqnarray} \left\{\begin{array}{l} v_2 &=& \displaystyle\frac{(ex-1)v_1+(e+1)xV_1}{x+1}\tag{3}\label{p2952eq3}\\ V_2 &=& \displaystyle\frac{-(e+1)v_1+(x-e)V_1}{x+1} \end{array} \right. \end{eqnarray}$$

と求めることができます。$e=1$ とすれば、参考文献と同じ値になっています。

検算

　検算をします。試験などのときにも、ややこしい式を解いた時には必ずするとよい検算です。それは、極端な場合を考えてみることです。「極端な場合」は直感的に理解しやすい場合が多いからです。ここでは簡単のために $e=1$ で考えます。

$x=0$: 自分のラケットが極端に軽い場合

　自分のラケットが極端に軽い場合とは、$M=0$ つまり、$x=0$ のことです。すると式$\eqref{p2952eq3}$は、

$$\begin{eqnarray} \left\{\begin{array}{l} v_2 &=& -v_1\tag{4}\label{p2952eq4}\\ V_2 &=& -2v_1-V_1 \end{array} \right. \end{eqnarray}$$

となります。

$v_2=-v_1$

　自分の返球したボールの速度 $v_2$ が負になっており、しかももとのボールの速さと同じ $v_1$ です。これは、ボールがそのままの速度で通過してしまったことを意味します。重さのないラケットで打ってもボールは跳ね返らないという結果で、直感に合います。またこれは、軽いラケットでは相手のボールに打ち負ける、ということを意味します。

$V_2=-2v_1-V_1$

　自分のラケットの速度 $V_2$ も負になっています。それも、もともと振り出していた速さ $V_1$ にボールの速さの2倍 $2v_1$ もの速さも加えて跳ね返されています。ラケットが跳ね返されており、軽いラケットでは手への衝撃が激しいことを意味します。

$x=\infty$: 自分のラケットが極端に重い場合

　この場合の式$\eqref{p2952eq3}$は、

$$\begin{eqnarray} \left\{\begin{array}{l} v_2 &=& v_1+V_1\tag{5}\label{p2952eq5}\\ V_2 &=& V_1 \end{array} \right. \end{eqnarray}$$

となります。$M=\infty$ の場合には実際にはラケットは静止していると考えると $V_1=0$ なので、式$\eqref{p2952eq5}$は

$$\begin{eqnarray} \left\{\begin{array}{l} v_2 &=& v_1\tag{6}\label{p2952eq6}\\ V_2 &=& 0 \end{array} \right. \end{eqnarray}$$

です。

$v_2=v_1$

　静止している壁にエネルギーの損失なしに跳ね返ったことを意味しており、直感に合います。重たいラケットを使えば、ラケットを振らなくてもそれなりにボールは返ることを意味します。

考察

理論的には6倍が最適

　簡単のために $e=1$ で考えます。

目的の再確認

　検算では $M=0$ と $M=\infty$ を考えましたが、実際には $M$ はその間であり手ごろな $V_1$ で打球していますから、跳ね返りの速度 $v_2$ は元の速度 $v_1$ よりも速く打ち返すことができます。ここでの目的はその比である $v_2/v_1$ を大きくすることであり、そのようなラケットとボールの重さの比 $x(=M/m)$ を求めることです。

相手とのエネルギーの比で考える

ここで、式$\eqref{p2952eq3}$の上側の式を $e=1$ として再掲します。

$$\begin{eqnarray} v_2 &=& \displaystyle\frac{(x-1)v_1+2xV_1}{x+1}\tag{3:上側再掲} \end{eqnarray}$$

$v_2/v_1$ を求めるためには $V_1$ を $v_1$ で表現できればよいです。$v_1$ と $V_1$ そのものはそれぞれ相手からのボールの速度と自分のラケットの速度で、両者を直接比べるのはやりにくいですが、それを2乗して重さを加味するとエネルギーの単位になり、どちらも人が与えたエネルギーが起源なので比較可能です。そこで、次の量を導入します。

$$\begin{eqnarray} \phi &=& \frac{\displaystyle\frac{1}{2}MV_1^2}{\displaystyle\frac{1}{2}mv_1^2}\tag{7}\label{p2952eq7} \end{eqnarray}$$

こうすることでどちらもエネルギーの単位になり、しかも分子は「自分がラケットに加えたエネルギー」、分母は「相手がボールに加えたエネルギー」となるので、つまりは自分と相手のエネルギーの比と置き換えたことになります。

結論の式

このように置くと $V_1$ は次のように表せます。

$$\begin{eqnarray} V_1 &=& v_1\sqrt{\frac{\phi}{\frac{M}{m}}}\\ &=& v_1\sqrt{\frac{\phi}{x}}\tag{8}\label{p2952eq8} \end{eqnarray}$$

これを式$\eqref{p2952eq3}$の $V_1$ に代入して両辺を $v_1$ で割ることにより、

$$\begin{eqnarray} y= \frac{v_2}{v_1} &=& \displaystyle\frac{(x-1)+2x\sqrt{\frac{\phi}{x}}}{x+1}\\ &=& \displaystyle\frac{(x-1)+2\sqrt{\phi x}}{x+1}\tag{9}\label{p2952eq9} \end{eqnarray}$$

が導かれます。

グラフ化

　式$\eqref{p2952eq9}$をグラフに表すと次のようになります $(e=1)$。例えば $\phi=1$ ではWolfram Alphaでもそのグラフを確認でき、さらには微分までしてくれています。この微分の値を $0$ にする $x$ の値は $x=5.8$ であり、このとき最も効率よく跳ね返すということになります。確かに、6倍に近い値です。

しかし一方で興味深いのは、

• $\phi$ の値により最適な比は異なる
• とはいっても、最適な値の幅は広い

点です。

$\phi$ の値により最適な比は異なる

　$\phi=1$ のときには最適な重さの比は $5.8$ であり6倍に近い値ですが、$\phi$ が大きくなると最適な値は小さくなります。$\phi$ が大きいとは自分の方がパワーが大きいということなので、自分の方が強い球を打つ場合には少し軽めのラケットの方がより強く打てるということを意味します(軽めのラケットの方が $V_1$ を大きくできるから)。反対に $\phi$ が小さい、つまり相手の方が強い球を打つ場合には少し重めのラケットの方が強く打てることを意味します(重めのラケットの方が力負けしにくいから)。

とはいっても、最適な値の幅は広い

　とはいっても、最適な値の幅は広いです。なので、ラケットとボールの重さの比が6近辺ならだいたいどのような重さのものを使ってもよいことを意味します。力のない人が力負けしにくいからとあまりに重たいラケットを持って走り回るのはナンセンスですし、強く打てるからとあまりに軽いラケットを使うのは肘への負担が大きくなります。

従って、ラケットとボールの重さの比は6倍程度が最適であることを基本として、力が無ければ少し重めのラケットが、力があれば少し軽めのラケットが理論的にはよいことを念頭に試してみて、最後は自分の肌感覚に合うものが最適ということが言えます。

まとめ

　衝突問題として扱い立式をしました。すなわち、運動量保存の法則と跳ね返り係数の式です(式$\eqref{p2952eq1}$)。

これを解くことで、ラケットとボールの重さの比 $\displaystyle\frac{M}{m}(=x)$ の関数として返球速度 $v_2$ を得ました(式$\eqref{p2952eq3}$)。

相手の打球速度 $v_1$ に対する比 $v_2/v_1$ を求めるために相手と自分のエネルギーの比 $\phi$ (式$\eqref{p2952eq7}$)を導入することにより、$\phi$ をパラメータとして解(式$\eqref{p2952eq9}$)を得ることができました。

これにより、

• $\phi=1$、つまり相手と自分の力が拮抗している場合にはラケットの重さはボールの重さの6倍がよいこと
• $\phi>1$、つまり自分の方が力が強い場合には軽めの方が、反対に
• $\phi<1$、つまり相手の方が力が強い場合には重めの方が強く返球できること
• とはいっても最適値の幅は広いので、あまり神経質になりすぎるのもよくないこと

が分かりました。

このように理論が分かった状態でラケットを選ぶのもまた楽しいですね。

関連記事

1. テクニカルテニス Rod Cross, Crawford Lindsey; 常盤 泰輔訳, p36 ↩︎