垂線の足を求める方法は一つだけではありません。
傾きの積を使う基本的な考え方から、法線ベクトルを使ったベクトル方程式、そして最速で求められる射影ベクトルまで、複数のアプローチがあります。
この記事では、同じ問題を「初級 → 中級 → 上級」と段階的に3つの方法で解説します。
計算量は多いけれど分かりやすい方法から、プログラムにも使いやすい射影ベクトルまで揃えていますので、自分に合った解き方を見つけてみてください。
なお、射影ベクトルの考え方は、
- 【直線に関して対称な点】
- 【点と直線の距離】
といった応用問題でもそのまま使えます。
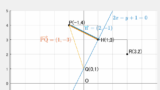
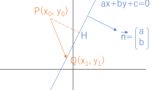
直線 $y=2x+1$ に点 $\mathrm{P}(-1,4)$ から下ろした垂線の足 $\mathrm{H}$ の座標を求めよ。
初級:傾きの積を利用する方法
考え方:傾きの積が $-1$
垂直に交わる直線の傾き同士を掛けると $-1$ になります。
つまり、傾き $-\displaystyle\frac{a}{b}$ の直線に垂直な直線の傾きは $\displaystyle\frac{b}{a}$ です。

青線の式を
$$y=-\displaystyle\frac{a}{b}x+\displaystyle\frac{c}{b}$$
と、ちょっと難しい式にしてしまっているのは、
次の「法線ベクトルを利用」の絵
$$ax+by=c$$
とそろえるためです。
計算例
直線 $y=2x+1$ に点 $\mathrm{P}(-1,4)$ から下ろした垂線の足 $\mathrm{H}$ の座標を求めよ。
点 $\mathrm{H}(a,b)$ と置くと、$\mathrm{PH}$ の傾きが $-\displaystyle\frac12$ になればよいので、
$$\frac{b-4}{a-(-1)}=-\frac12 \tag{1}\label{p1362eq1}$$
また、$\mathrm{H}$ は直線 $y=2x+1$ 上にあるので
$$b=2a+1 \tag{2}\label{p1362eq2}$$
\eqref{p1362eq1}, \eqref{p1362eq2} を解いて
$$\mathrm{H}(1,3)$$
中級:ベクトル方程式を利用する方法
ベクトル方程式とは
3次元版ですが、こちらにまとめています。
法線ベクトルとは
ある直線や平面に対して垂直なベクトルです。
法線ベクトルは $ax+by=c$ の係数
直線
$$ax+by=c$$
に垂直なベクトル(法線ベクトル)は
$$\begin{pmatrix}a \\ b\end{pmatrix}$$
です。

これは3次元でも同様で、平面
$$ax+by+cz=d$$
の法線ベクトルは
$$\begin{pmatrix}a \\ b \\ c\end{pmatrix}$$
です。
考え方:$\mathrm{H}$ を与える媒介変数値を求める
$\mathrm{P}$ から $\begin{pmatrix}2 \\ -1\end{pmatrix}$ 方向にどれだけ進めば $\mathrm{H}$ に到達するか、ということです。
計算例
直線 $y=2x+1$ に点 $\mathrm{P}(-1,4)$ から下ろした垂線の足 $\mathrm{H}$ の座標を求めよ。
直線 $2x-y=-1$ の法線ベクトルは $\begin{pmatrix}2 \\ -1\end{pmatrix}$。
点 $\mathrm{P}(-1,4)$ を通りこの方向に進む直線は
$$\begin{pmatrix}x \\ y\end{pmatrix}=\begin{pmatrix}-1 \\ 4\end{pmatrix}+t\begin{pmatrix}2 \\ -1\end{pmatrix}$$
これが $2x-y=-1$ に交わるのは $t=1$ のとき。
$$\therefore\;\mathrm{H}(1,3)$$
補足:共通テストでの類題
24年度共通テストでは、3次元のベクトル方程式を扱う問題が出題されました。
(内積ゼロがミソの問題です。IIB-第5問)
上級:射影ベクトルを利用する方法(本命)
射影ベクトルとは
「射影ベクトル」は、あたかも真上から光を当ててできる影のようなベクトルです。
垂線の足を一発で求められる最速の方法です。

$$\overrightarrow{\mathrm{OH}}=\frac{\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}}}{|\overrightarrow{\mathrm{OA}}|^2}\cdot\overrightarrow{\mathrm{OA}}\tag{1-1}\label{p1362eq1-1}$$
なぜこの右辺が $\overrightarrow{\mathrm{OH}}$ を表すのか?
$\overrightarrow{\mathrm{OH}}$ の向きは $\overrightarrow{\mathrm{OA}}$ の向き
まず、\eqref{p1362eq1-1}は、
$$\overrightarrow{\mathrm{OH}}=\alpha\cdot\overrightarrow{\mathrm{OA}}$$
の形をしています。これは、
$\overrightarrow{\mathrm{OH}}$ の向きは $\overrightarrow{\mathrm{OA}}$ の向き
ということを表しています。
$\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}}=|\overrightarrow{\mathrm{OH}}||\overrightarrow{\mathrm{OA}}|$
これは内積の図形的意味です。
$\overrightarrow{\mathrm{OH}}=\displaystyle\frac{\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}}}{|\overrightarrow{\mathrm{OA}}|}\cdot\frac{\overrightarrow{\mathrm{OA}}}{|\overrightarrow{\mathrm{OA}}|}$ と見る
このように見ると、ここに「内積の図形的意味」の、
$$\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}}=|\overrightarrow{\mathrm{OH}}||\overrightarrow{\mathrm{OA}}|$$
を代入することにより、
$$\overrightarrow{\mathrm{OH}}=|\overrightarrow{\mathrm{OH}}|\cdot\frac{\overrightarrow{\mathrm{OA}}}{|\overrightarrow{\mathrm{OA}}|}$$
です。
$\overrightarrow{\mathrm{OH}}$ は 向きが $\overrightarrow{\mathrm{OA}}$ で大きさが $|\overrightarrow{\mathrm{OH}}|$ のベクトル
ここで、
$$\frac{\overrightarrow{\mathrm{OA}}}{|\overrightarrow{\mathrm{OA}}|}$$
の大きさは $1$ です。これに $|\overrightarrow{\mathrm{OH}}|$ を掛けているので、
$\overrightarrow{\mathrm{OH}}$ は 向きが $\overrightarrow{\mathrm{OA}}$ で大きさが $|\overrightarrow{\mathrm{OH}}|$ のベクトル
を意味し、確かに正しいです。
考え方:直線方向への射影
$\overrightarrow{\mathrm{QA}}$ 上に $\overrightarrow{\mathrm{QP}}$ を射影します。
なお、$\overrightarrow{\mathrm{QA}}$ はより単純な $\begin{pmatrix}1 \\ 2 \end{pmatrix}$ でもかまいませんが、
求めるべき $\overrightarrow{\mathrm{QH}}$ との混同を避けるため、あえて $\begin{pmatrix}2 \\ 4 \end{pmatrix}$ にしています。
(自分でやるときは $\begin{pmatrix}1 \\ 2 \end{pmatrix}$ でかまいません。)
計算例(直線方向への射影)
直線 $y=2x+1$ に点 $\mathrm{P}(-1,4)$ から下ろした垂線の足 $\mathrm{H}$ の座標を求めよ。
点 $\mathrm{Q}(0,1)$、$\mathrm{A}(2,5)$ とすると、$\mathrm{P}(-1,4)$ とから、
$$\begin{eqnarray}
\overrightarrow{\mathrm{QH}} &=& \frac{\overrightarrow{\mathrm{QA}}\cdot\overrightarrow{\mathrm{QP}}}{|\overrightarrow{\mathrm{QA}}|^2}\cdot\overrightarrow{\mathrm{QA}}=\frac{\begin{pmatrix}2 \\ 4 \end{pmatrix}\cdot\begin{pmatrix}-1 \\ 3 \end{pmatrix}}{\left|\begin{pmatrix}2 \\ 4 \end{pmatrix}\right|^2}\cdot\begin{pmatrix}2 \\ 4 \end{pmatrix}\\
&=& \begin{pmatrix}1 \\ 2 \end{pmatrix}
\end{eqnarray}$$
$\mathrm{Q}$ の座標が $(0,1)$ なので、
$$\mathrm{H}(1,3)$$

補足(向きが逆でもOK)
$\overrightarrow{\mathrm{QA}}$ の向きは逆でも同じ結果になります。
考え方:法線方向への射影(本命)
$\overrightarrow{n}$ 上に $\overrightarrow{\mathrm{PQ}}$ を射影します。
計算例(法線方向への射影)
直線 $y=2x+1$ に点 $\mathrm{P}(-1,4)$ から下ろした垂線の足 $\mathrm{H}$ の座標を求めよ。
$2x-y+1=0$ の法線ベクトルは $\overrightarrow{n}=\begin{pmatrix}2 \\ -1\end{pmatrix}$。
直線 $y=2x+1$ 上の点の一つ $(0,1)$ を $\mathrm{Q}$ と置くと、
$$\begin{eqnarray}
\overrightarrow{\mathrm{PH}} &=& \frac{\overrightarrow{\mathrm{PQ}}\cdot\overrightarrow{n}}{|\overrightarrow{n}|^2}\cdot\overrightarrow{n}= \frac{\begin{pmatrix}1 \\ -3 \end{pmatrix}\cdot\begin{pmatrix}2 \\ -1 \end{pmatrix}}{\left|\begin{pmatrix}2 \\ -1 \end{pmatrix}\right|^2}\cdot\begin{pmatrix}2 \\ -1 \end{pmatrix}\\
&=& \begin{pmatrix}2 \\ -1 \end{pmatrix}
\end{eqnarray}$$
$\mathrm{P}$ の座標が $(-1,4)$ なので、
$$\mathrm{H}(1,3)$$

補足(向きが逆でもOK)
$\overrightarrow{n}$ を逆向きにしても同じ結果になります。
まとめ:状況別のおすすめ解法
| 状況 | 方法 | 理由 |
|---|---|---|
| 基本を理解したい | 初級:傾きの積 | 理屈が簡単 |
| 計算量を減らしたい | 中級:ベクトル方程式 | 理屈が比較的簡単で手順が短い |
| 最速で求めたい | 上級:射影ベクトル | ほぼ一発で求まる |
点と直線の距離は、射影ベクトル(法線方向)で最もスマートに求められます:






コメント