過去問は「解いて終わり」ではなく、繰り返し解くことで本質が見えてくる教材です。共通テストの物理は特に、基礎の“核”を丁寧に問う良問が多く、早い段階で触れることで 何が重要なのか が自然と浮かび上がってきます。
そこでこのページでは、2024年度の共通テスト物理から 本質をつかむための典型5題 を厳選しました。力学・熱・波・運動量・電磁気と幅広い分野を扱っていますが、どれも「繰り返し復習する価値のある問題」です。
読むたびに理解が深まり、読むときには見える景色が変わる──そんな学び方ができる構成にしています。
同様に数学もありますので合わせてご覧ください。
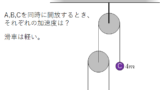
第1問-1 モーメントのつりあい
直角二等辺三角形の板 $\mathrm{ABC}$ がある。
点 $\mathrm{B}$ に水平右向きの力 $F$ を加える。
板が点 $\mathrm{A}$ のまわりで回転しない $F$ の最大値を求めよ。

力 $F$ を増してもしばらくは板は動きません。力のつり合いとモーメントのつり合いが保たれているからです。垂直抗力 $N_1$ はモーメントがつり合うように作用点が変化し、右端まで行った瞬間に支えられなくなって回転します。
したがって、$N_1$ が右端まで行ったところが力 $F$ の最大値です。
解:$N_1$ が右端まで行く $F$
力 $F$ が最大のとき、図の状態でつり合っている。

点 $\mathrm{A}$ の周りのモーメントのつり合いより
$$F \cdot L = Mg \cdot \frac{2}{3}L$$
$$\therefore\; F = \frac{2Mg}{3}$$
解説:力の描画とつりあいの考え方
- 重力:重心から $Mg$
- 床からの垂直抗力:$N_1$
- 壁からの反力:$N_2$
- 外力:点 B に水平右向きの $F$
力のつり合いより
$$Mg = N_1,\qquad F = N_2$$
力の描画のコツは別記事でも扱っています。
解説:モーメントのつりあい
モーメントは
モーメント = 力 × 腕の長さ
であり、平行四辺形の面積としてイメージすることができます。
回転軸はどこを取ってもよく、未知数が消える点 $\mathrm{A}$ を取るのが自然です。
解説:回転軸はどこでもよい
例えば重心を回転軸に取ると
$$F\cdot\frac{2}{3}L + N_2\cdot\frac{1}{3}L = N_1\cdot\frac{2}{3}L$$
ここに $N_1=Mg,\; N_2=F$ を代入すると
$$F\cdot L = Mg\cdot\frac{2}{3}L$$
となり、同じ結果が得られます。
回転軸はどこでもよいが、結果は変わらないという良い確認になります。
第1問-2 気体分子運動論
太陽の中心部の温度は約1500万Kであり、そこには水素原子核やヘリウム原子核が電子と結びつかずに存在している。その状態を、単原子分子理想気体とみなすとき、
(1) 太陽の中心部にあるヘリウム原子核1個あたりの運動エネルギーの平均値は、温度300Kの空気中に、単原子分子理想気体として存在するヘリウム原子1個あたりの運動エネルギーの平均値の何倍か。
(2) 太陽の中心部で、水素原子核1個あたりの運動エネルギーの平均値は、ヘリウム原子核1個あたりの運動エネルギーの平均値の何倍か。
単原子分子理想気体では内部エネルギーは
$$U=\frac{3}{2}nRT$$
で表され、分子の運動エネルギーの総和が内部エネルギーです。
【気体分子運動論】一行でサクッと導出 内部エネルギーと分子の運動エネルギー | 人に教えたくなる数学
したがって
分子1個あたりの運動エネルギー $\propto T$
となり、原子の種類には依存しません。
解(1):運動エネルギーの比
$$\frac{1.5\times 10^7}{300} = 5\times 10^4$$
よって 5万倍。
解(2):水素とヘリウムの比較
運動エネルギーは温度だけの関数なので、同じ温度なら同じです。
したがって 1倍。
解説:問題文は長いが、単原子分子理想気体という条件を言いたいだけ
単原子分子理想気体
- 原子核が電子と結びつかずに存在している。その状態を単原子分子理想気体とみなす
- 単原子分子理想気体として存在するヘリウム原子核
といった表現は長くて少しうんざりしますが、実は単に「単原子分子理想気体ですよ」と言いたいだけです。「はいはい、単原子分子理想気体を言いたいのね」と優しい気持ちで読めばOKです。入試問題なので丁寧に書かざるを得ないだけです。
運動エネルギーの平均値
同じように「運動エネルギーの平均値」という表現も、実際には分子の速さはバラバラであることを暗に言っていますが難しく考えずに、単に「運動エネルギー」として扱えば十分です。
解説:単原子分子理想気体とはどういう気体か?
この言葉には次の2つの意味が含まれています。
- 単原子分子
- 理想気体
単原子分子
文字通り、1つの原子だけでできた分子です。ヘリウムやアルゴンなどの希ガスが代表例です。窒素(N2)や酸素(O2)は2原子分子なので該当しません。
単原子分子でない場合、内部エネルギーには分子の回転や振動のエネルギーも含まれ、複雑になります。(だから入試ではまず出ません。出ても丁寧な誘導がつきます。)
理想気体
分子間の相互作用が無いとみなせる気体です。平たく言うと、「ぶつからないくらい希薄」ということです。
私たちが普段吸っている空気も、体積比で 1/1000 程度の密度なので十分に希薄で、理想気体として扱えます。
第1問-3 全反射
図において臨界角 $\sin\theta_c$ を求めよ。


屈折の法則は
$$n_1\sin\theta_1 = n_2\sin\theta_2$$
です。この関係をホイヘンスの原理から理解する下記の記事も見てください。
水から空気への境界で、屈折角 $\theta_2 = 90^\circ$ となるときの入射角が臨界角です。
解:臨界角の導出

図より
$$\sin\theta_c = \frac{1}{n_1}$$
解説:水面の臨界角
水の屈折率は $n_1=1.33$ なので
$$\sin\theta_c = \frac{1}{1.33}$$
を満たす角度が臨界角で、およそ $49^\circ$ です。
水中から外を見ると、これより浅い角度では全反射して外が見えません。下の図で外の景色が円形内部にすべて見えていてその外側は見えていないのはこの臨界角によるものです。
スネルの窓 – Wikipedia
第2問-4 運動量保存の法則
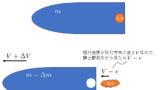
ペットボトルの中には水と圧縮空気が入っている。$t=0$ で水の噴射を開始した。短い時間 $t=\Delta t$ で質量 $\Delta m$ の水が速さ $u$ で噴出した。
このとき、ペットボトルの速さ $\Delta v$ を求めよ。
ただし、$\Delta m$ は $M$ に比べて小さいため、$M-\Delta m\simeq M$ と考えてよい。また、重力や空気抵抗は無視する。

解:ペットボトルロケットの速度変化
運動量保存より
$$0 = M\Delta v – \Delta m u$$
$$\therefore\; \Delta v = u\frac{\Delta m}{M}$$
解説:ツィオルコフスキーのロケット方程式
燃料を後方に噴射することで前進する──そのことを記述する法則が 運動量保存の法則 です。
この考え方は実際のロケットにも使われています。
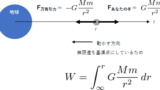
第4問-1 電場と電位
真空中に大きさが同じで符号が逆の二つの点電荷が作る等電位面の模式図を選択肢から選べ。
選択肢:

解:等電位面の模式図
電位の式は
$$V = k\frac{Q}{r}$$
で、これを図示するとこのようになる。
よって、②が正解。

解説:電位の反比例構造と選択肢の見方
- 電位は距離の反比例
- 正電荷は正の山、負電荷は負の谷
このイメージがあれば、迷わず選べます。
参考記事:下記の「電位」
まとめ:典型問題を通して本質をつかむ
過去問は一度解いて終わりではなく、繰り返し解くことで本質が見えてくる教材です。共通テストの物理は、基礎の“核”を丁寧に問う良問が多く、今回扱った5題もその典型です。
ここで扱った問題を繰り返し復習することで、
- 何が重要なのか
- どこが本質なのか
- どの知識が幹になるのか
が自然とつかめるようになります。
ぜひ、この5題を軸に理解の幹を太くしていってください。








コメント