過去問は「同じ問題は出ない」「一部だけ解いても意味がない」と思われがちですが、共通テストの過去問は基礎の本質を問う良問が多く、繰り返し解くほど力がつきます。
過去問を軸に周辺知識を広げていくことで、理解の“幹”が太くなり、どんな問題にも対応できる土台ができます。
この記事は、そんな「何度も解きたくなる過去問」を目指して作りました。 手を動かすたびに理解が深まる、その感覚を一緒に積み重ねていきましょう。
各題名は、実際の共通テストの問題番号を示しています。
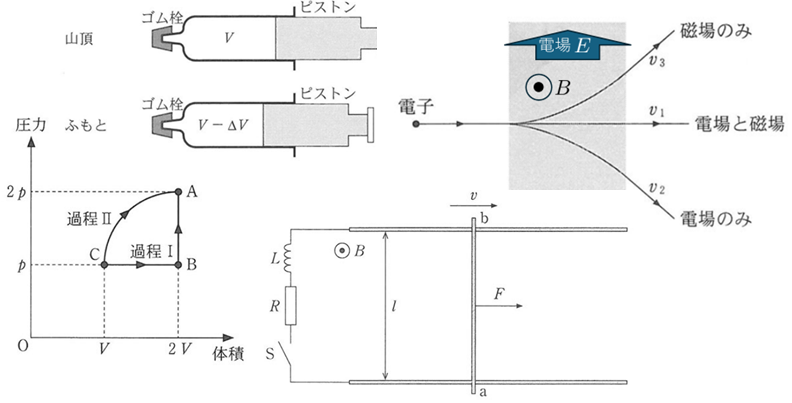
第1問-1 状態方程式
$P_0$ を $P_1$, $V$, $\Delta V$, $T_0$, $T_1$ で表せ。

解. 山頂の圧力 $P_0$
山頂とふもとで状態方程式を書き、比を取るだけです。
$$P_0V=nRT_0,\qquad P_1(V-\Delta V)=nRT_1$$
両辺を割って整理すると、
$$P_0=\frac{P_1(V-\Delta V)T_0}{VT_1}$$
第3問 状態方程式:P–V図
物質量 $n$ の理想気体をゆっくり変化させる。気体定数は $R$。
(1) 図1の $\rm{A}\rightarrow\rm{B}\rightarrow\rm{C}$ において、状態 $\rm{A}$ の温度を $T_A$ とするとき、気体が外部にした仕事を $n$, $R$, $T_A$ で表せ。

(2) この過程を $T-V$ 図で表せ。$\rm{B}$ の温度は $T_B$、$\rm{C}$ は $T_C$ としてよい。
(3) $\rm{A}\rightarrow\rm{B}\rightarrow\rm{C}$ を逆にした過程 $\rm{I}$ と、図2の $\rm{C}\rightarrow\rm{A}$ の過程 $\rm{II}$ を比較し、外部から加えられた熱量はどちらが大きいか。

解(1). A→B→C の仕事
点Aの状態方程式は
$$2p\cdot 2V=nRT_A$$
気体が外部にした仕事は $W=-pV$ なので、
$$W=-pV=-\frac14 nRT_A$$
解説:別の状態への変換
$P-V$ 図の面積が仕事です。今回は長方形の面積を $nRT_A$ に変換するだけの問題です。

解(2). T-V図への変換
下図のようになります。

解説:定積と定圧の変換
定積
$\rm{A}\rightarrow\rm{B}$ は体積一定なので縦線。

定圧
$\rm{B}\rightarrow\rm{C}$ は定圧変化なので $V\propto T$ の直線になります。
($PV=nRT$ で $P$ 一定なら $V\propto T$)

解(3). 過程 I と II の熱量比較
熱力学第一法則 $Q=\Delta U+W$ を使います。
内部エネルギーは温度だけの関数(下記解説参照)。温度変化量が同じなので、内部エネルギー変化量も同じ。よって、$\Delta U_I=\Delta U_{II}$。
一方、$W$ は $P-V$ 図の面積なので、図より $W_I<W_{II}$。
よって、
$$Q_I<Q_{II}$$
解説:仕事をした分だけ多くの熱量が必要
直感的には、
過程 $\mathrm{II}$ の方が仕事をたくさんしているのでその分熱もたくさん使っている
ということです。
解説:内部エネルギーは温度だけの関数
単原子分子ならば
$$U=\frac{3}{2}nRT$$
なので、内部エネルギーは温度だけで決まります。単原子分子でない場合でも、定数が $\displaystyle\frac{3}{2}$ ではないだけで、温度だけの関数であることは変わらないです。
参考記事:
第1問-4 電磁気:ローレンツ力
電子が電場と磁場の中を通過する。直進したときの速さを $v_1$、電場のみのときを $v_2$、磁場のみのときを $v_3$ とする。$v_1$, $v_2$, $v_3$ の大小関係を述べよ。

解. 速さの大小関係
磁場では速さは変わらないので $v_1=v_3$。
電場では加速するので $v_2>v_1$。
よって、
$$v_2>v_3=v_1$$
解説:磁場では速さは変わらない
磁場によって電子が受ける力は常に速度に対して垂直方向なので、速さは変わりません。
その分向きは変わり、円運動をします。
第4問 電磁気:導体棒の移動
ここは下記記事と深くつながる内容です。誘導起電力 → 電流 → 電磁力 → エネルギー の流れを意識して解きましょう。
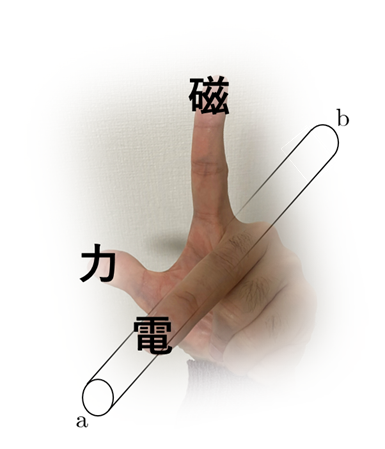
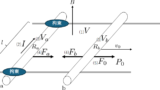
(1) 図1の初期状態からスイッチ S を閉じる。導体棒の速さ $v$ を保つために外力 $F$ を加える。
初期状態:コンデンサーは空、S は開
- ab間の誘導起電力 $V_1$
- S閉直後のab間の電流の向き
- 外力 $F$ のグラフ(選択肢)
- $t=\infty$ での外力の仕事 $W$、コンデンサーのエネルギー $U$、ジュール熱 $J$
ヒント:外力の仕事 $W$ は、十分な時間がたった時にコンデンサーに蓄えられている電荷を、導体棒の両端に生じる電位差 $V_1$ に逆らって運ぶ仕事に等しい。

(2) 図2の初期状態からスイッチ S を閉じる。導体棒の速さ $v$ を保つために外力 $F$ を加える。電流の大きさは図3のようになった。このとき、導体棒のab間に生じる誘導起電力を $V_2$ とする。
初期状態:スイッチ S は開
- $t=\infty$ でのコイルに発生する誘導起電力の大きさ
- 外力 $F$ を表すグラフ(選択肢)
- コイルの自己インダクタンス $L$ ($a$ を用いて)


選択肢:

解(1)-1. 誘導起電力
$$V_1=vBl$$
解(1)-2. 電流の向き
電流による力が外力 $F$ と逆向きになるように電流が流れる。
フレミング左手の法則より、
$$\rm{b\rightarrow a}$$
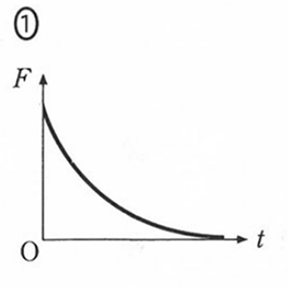
解(1)-3. 外力 $F$ のグラフ
S を閉じた直後 $t=0$ と、十分時間がたった後 $t=\infty$ を考えれば十分です。それも、滑らかなグラフになるはずです。
- $t=0:$ 電流が流れ外力が必要。
- $t=\infty:$ コンデンサに十分電気がたまるため電流は流れず、外力は 0。
解(1)-4. $W$, $U$, $J$
コンデンサーの電荷は $Q=CV_1$。
外力の仕事:問題文のヒントより
ヒント:外力の仕事 $W$ は、十分な時間がたった時にコンデンサーに蓄えられている電荷を、導体棒の両端に生じる電位差 $V_1$ に逆らって運ぶ仕事に等しい。
$$W=QV_1=CV_1^2$$
コンデンサーのエネルギー:公式より
$$U=\frac12 CV_1^2$$
ジュール熱:
$$J=W-U=\frac12 CV_1^2$$
解(2)-1. 十分時間がたったときの誘導起電力
十分に時間がたてば電流は一定。コイルはただの導線となる。よって誘導起電力の大きさは
$$0$$
解説:コイルの気持ち
コイルの正体は、ただの導線です。それをグルグルと巻いているだけです。そのことにより、変化を嫌うという性質が生まれ、誘導起電力という形で現れます。変化は嫌うが、徐々に電流は流れてきてしまいます。そのうち一定の電流が流れるようになれば、もう変化はなくなるので抵抗しなくなり、ただの導線に戻ります。
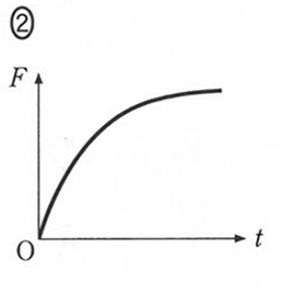
解(2)-2. 外力 $F$ のグラフ
S を閉じた直後 $t=+0$ と、十分時間がたった後 $t=\infty$ を考えれば十分です。それも、滑らかなグラフになるはずです。
- $t=+0$:コイルは電流の変化を妨げるため、電流はほぼ流れない。よって棒には電磁力が働かず、一定速度 $v$ を保つために必要な外力は 0。
- $t=\infty$:コイルはただの導線となり電流が流れる。よって棒には電磁力が働き、一定速度 $v$ を保つためには外力が必要。
解説:エネルギーの観点から考えてみる
$t>0$ では一定速度 $v$ を保つためには外力が必要ですが、この外力は回路に電流が流れることによる電磁力に抗うものです。回路には電流が流れていることにより、抵抗でエネルギーが消費され続けていますが、このエネルギー源こそが、外力です。
解(2)-3. コイルの自己インダクタンス $L$ ($a$ を用いて)
$t=0$ のとき、
- $I-t$ グラフの傾き $a$。
- 導体棒のab間に生じる誘導起電力 $V_2$。

$I-t$ グラフの傾き $a$ より、
$$\frac{dI}{dt}=a$$
誘導起電力の式から、
$$V_2=L\frac{dI}{dt}$$
よって、
$$V_2 = La$$
$$\therefore\; L = \frac{V_2}{a}$$
まとめ:典型問題を通して本質をつかむ
今回扱った問題は、どれも「典型的な流れ」を押さえることで一気に解きやすくなるものばかりです。状態方程式では比をとる発想、P–V図では面積=仕事、ローレンツ力では速さは変わらない、導体棒では誘導起電力 → 電流 → 電磁力 → エネルギーの流れ。この4つを繰り返し解くことで、自然と手が動くようになります。
電磁誘導の基礎や、今回の内容とつながるテーマは下記の記事で整理していますので、合わせて復習してください。




コメント