【屈折の法則】ホイヘンスの原理で徹底理解 公式は覚えるよりもイメージで

　私は常々「数学はイメージだ！」と言っています。物理ももちろん同じです。数式からではなく、物理現象をイメージで捉えられるようになることが大事です。

例えばすぐ下の問題のような場合、$\theta_1<\theta_2$ なのか $\theta_1>\theta_2$ なのかはイメージで理解できるようにしたいです。

この投稿では、ホイヘンスの原理をアニメーションを通じて理解することにより、これらのイメージを得ることを目的にします。

この問題は24年度の共通テストで出ました。下記の記事↓の「第1問-3」です。

典型的な問題で理解したい内容を確認

テストでの解答

$n_1\sin\theta_1 = n_2\sin\theta_2$ より、

$$\begin{eqnarray} \sqrt{3}\sin 30^\circ &=& 1\cdot\sin\theta_2\\ \sin\theta_2 &=& \frac{\sqrt{3}}{2}\\ \therefore\;\theta_2 &=& 60^\circ \end{eqnarray}$$

次章で $\theta_1<\theta_2$ をイメージ理解しよう

　上記の計算により確かに $\theta_1<\theta_2$ なのですが、この大小関係は計算しなくてもイメージで分かるようにしたいです。それが次に示すホイヘンスの原理です！

ホイヘンスの原理を用いて理解する

　ホイヘンスの原理とは、

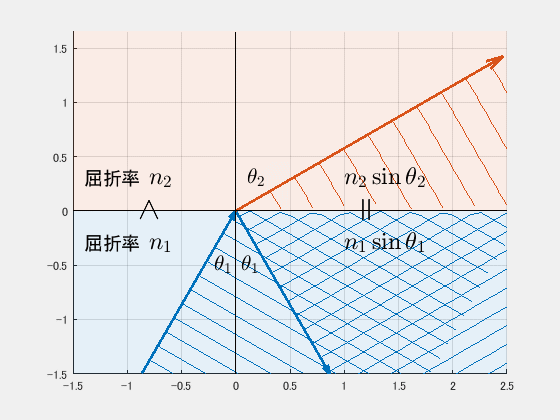
というものです。これを $y=0$ での反射・屈折面に適用したアニメーションが下記↓です。

ポイントは屈折率です。屈折率により波の進む速さが変わります。屈折率は、波の進行に対する抵抗値のようなもので、屈折率が大きいほど進行速度が遅いです。このことを踏まえ、屈折を理解します。

屈折

　屈折率が $n_1>n_2$ なので、$n_2$ の方が速く進みます。屈折率は抵抗のようなイメージで捉えましょう。抵抗が小さいので速く進む、というイメージです。

実際、上記のアニメーションでもそうなっていますね。広がる円の速さが下側と上側とで異なり、上側の方が速く広がっています。これにより、その包絡線である波面は $n_1$ とは異なる角度になっています。

そして結果として、

$$n_1\sin\theta_1=n_2\sin\theta_2$$

が成り立ちます。

反射

　反射では、当然ながらその前後に於いて媒体は変わらず屈折率は $n_1$ のままのため、屈折の前後で波の速さは変わりません。

従ってアニメーションでも明らかなようにその包絡線の角度は変わらず、入射角と反射角はどちらも $\theta_1$ です。

特殊な条件での反射

臨界角

　臨界角とは屈折後の角度が $90^\circ$ になるような入射角です。入射角を徐々に変えたときの屈折の様子を↓のアニメーションで確認します。

アニメーションは、入射角 $\theta_1$ を徐々に大きくしています。それに伴い屈折角 $\theta_2$ が大きくなりますが、屈折角 $\theta_2$ の方が入射角 $\theta_1$ よりも大きいため、途中で $\theta_2=90^\circ$ が訪れます。これが臨界角です。

そしてここに来るまでずっと

$$\sqrt{3}\,\sin\theta_1 = 1\,\sin\theta_2$$

が満たされています。臨界角では $\theta_2=90^\circ$ なので、

$$\sqrt{3}\,\sin\theta_1 = 1\,\sin 90^\circ$$

となり、この式から $\theta_1$ が割り出せる、というわけです。

全反射

　臨界角を超えて浅い角度で入射すると全反射します。その様子を↓のアニメーションで確認します。

臨界角までは

$$\sqrt{3}\,\sin\theta_1 = 1\,\sin\theta_2$$

が成り立つような $\theta_2$ が存在していますが、そこを超えると左辺の値が $1$ を超えるため、それに対応する $\theta_2$ が存在しなくなります。これが全反射の状態です。

水の場合

　水の場合は、$n_1=1.33$ なので、臨界角となる $\theta_1$ は、

$$\begin{eqnarray} 1.33\,\sin\theta_1 &=& 1\sin 90^\circ\\ \sin\theta_1 &=& \frac{1}{1.33}\\ \therefore\,\theta_1 &\simeq& 49^\circ \end{eqnarray}$$

です。つまり、$49^\circ$ よりも浅い角度で水中から眺めると全反射してしまい外を見ることができません。このように見えます。

スネルの窓 – Wikipedia

まとめ

　反射と屈折、そして臨界角と全反射について見てきました。重要な式は

$$n_1\sin\theta_1 = n_2\sin\theta_2$$

です。屈折率 $n_1$, $n_2$ は通常の問題では与えられることが多く、臨界角 $\theta_1$ を求めさせる問題が多いです。臨界角では $\theta_2=90^\circ$ なのでそこから $\theta_1$ が求められます。

そしてまずはホイヘンスの原理から屈折角が入射角よりも大きくなるのか、小さくなるのか、イメージで理解できることが重要です。

実際の問題↓で確かめてみましょう。「第1問-3」です。